It can be argued, reasonably enough, that using classifier ensembles instead of a single well thought out classifier is disadvantageous because of the corresponding increases in computational demands and implementation complexity. This argument appears particularly convincing when one considers the reality that there can often be no guarantee that an ensemble of classifiers will perform better than the best of its component classifiers. The additional complexity introduced by an ensemble is particularly problematic in cases where one is interested in analyzing the trained classifiers as well as simply using them.
Furthermore, as argued by Ho (2002), an excessive research emphasis on classifier combination can potentially cause one to become so involved in the details and complexities of ensemble coordination that one looses sight of the fundamental problem of classification. One must therefore be careful to avoid overzealously embracing sophisticated ensemble classification methodologies without a convincing understanding of why doing so is beneficial to the particular task at hand.
Despite the validity of these concerns, however, there are a number of important reasons why ensemble classification can in fact be a better choice than a single well-chosen classifier. Dietterich (2000) has organized these reasons into three categories:
Suppose one has a number of classifiers, each trained on a labelled data set. One knows how well they each performed on the training, testing and potentially the validation data, but this is only an estimate of how well they will generalize to the universe of all possible inputs, not a guarantee. If all of the classifiers performed similarly on the testing and validation data, one has no way of knowing which is the best in truth. If one simply chooses a single such classifier randomly, one runs the risk of accidentally choosing the worst one. Combining the results of all of the classifiers will most likely perform at least as well as the average classifier. Although the ensemble may or may not perform better or even as well as the best individual classifier, one cannot be sure ahead of time which one is in fact the best if they performed similarly individually on the test and validation data.
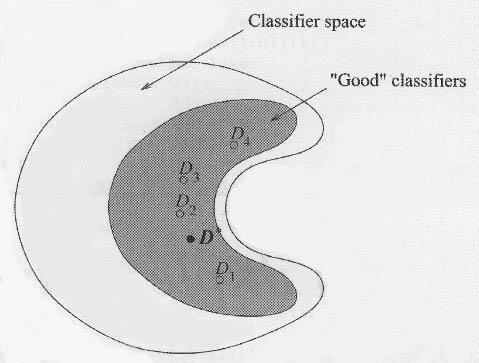
The statistical argument is illustrated graphically in Figure 2.1. Suppose one has four trained classifiers, D1 through D4, and D* is the theoretically optimal classifier. If one somehow knew where each of these classifiers were in classifier space, and one also somehow knew where D* was, then one might choose to use only D2, as it is the closest to D*. Of course, in reality, one has no way of knowing this. The option of combing the classifiers into an ensemble can result in an aggregated classifier that is likely to perform better than one of the classifiers chosen randomly.
The statistical argument for using classifier ensembles is particularly strong in cases where only limited training and testing data is available. This is because the evaluation of individual classifiers using test sets is likely to have a high variance because of high dependence on the particular training and testing instances due to their small number. This variance implies a large corresponding uncertainty in the evaluation of each component classifier, which means that one can be unsure of which will perform best in the full universe of possible input patterns. The use of a classifier ensemble in a case such as this helps to guard against the possibility of happening to choose a particularly bad classifier based on a misleadingly high performance on a small and non-representative test set.

Figure 2.1: The statistical reason for combining classifiers. D1 through D4 are trained classifiers and D* is the theoretically optimum classifier. The shaded area represents the area in classifier space of classifiers that perform well on a given data set (Kuncheva 2004, p. 102).
The computational argument is illustrated in Figure 2.2. Each of the classifiers D1 through D4 move closer during training to the theoretically optimum classifier (D*) from their initial pre-training locations in classifier space. Each of D1 through D4 offers a different solution after training, and combining these solutions can result in better solution overall than the solution offered by any of the individual classifiers.
The computation argument highlights the particular appropriateness of instable classifiers for ensemble classification. Instable classifiers are classifiers where small changes in the training set can have a significant effect on the classifier output. The use of multiple instable classifiers trained on slightly different but potentially overlapping training sets can lead to a variety of useful solutions that can be fruitfully combined.

Figure 2.2: The computational reason for combining classifiers. D1 through D4 are hill climbing classifiers and D* is the theoretically optimum classifier. The dashed lines show the trajectories of each classifier during training (Kuncheva 2004, p. 103).
An alternative solution to the non-linear problem presented above, of course, would be to use a more sophisticated single classifier. One must remember, however, that the primary disadvantage of using classifier ensembles over single classifiers is that they introduce added complexity to the solution. It may well be that an ensemble of simple classifiers can perform faster and be implemented more easily and intuitively than a single complex classifier. The argument against using classifier ensembles is therefore reversed in cases such as this.
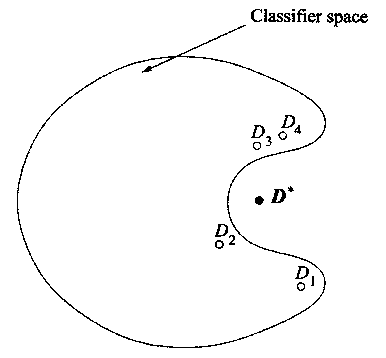
Figure 2.3: The representational reason for combining classifiers. The closed shape represents the range of classifiers that one is able or willing to construct. D1 through D4 represent four trained classifiers and D* represents the theoretically optimal classifier. (Kuncheva 2004, p. 104).
![]()
Next: Classifier ensemble design issues
![]()
Last modified: April 18, 2005.
-top of page-