Next: Diameter and Taper Discontinuities Up: Conical Air Column Modeling Previous: Reflection at a Rigid Boundary
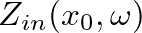 for this system can be determined by calculating its response to a unit volume velocity impulse and transforming it to the frequency domain using the DFT.
for this system can be determined by calculating its response to a unit volume velocity impulse and transforming it to the frequency domain using the DFT.
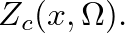
![$\displaystyle h^{+}(x,t) = \frac{\rho c}{A(x)}\left[ \delta(t) - \frac{c}{x} \,e^{-(c/x)t}\epsilon(t)\right],
$](img137.png) (26)
(26)
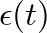 is the Heaviside unit step function.
is the Heaviside unit step function.
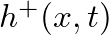 in the discrete-time domain.
in the discrete-time domain.
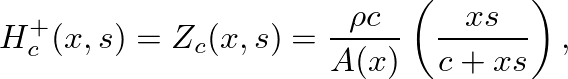 (27)
(27)
 is the spherical-wave surface area at
is the spherical-wave surface area at 
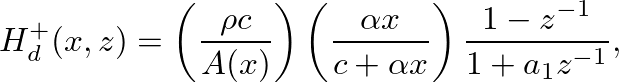 (28)
(28)
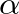 is the bilinear transform constant and
is the bilinear transform constant and 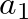 is equal to the allpass truncation filter coefficient given in Eq. (25).
is equal to the allpass truncation filter coefficient given in Eq. (25).
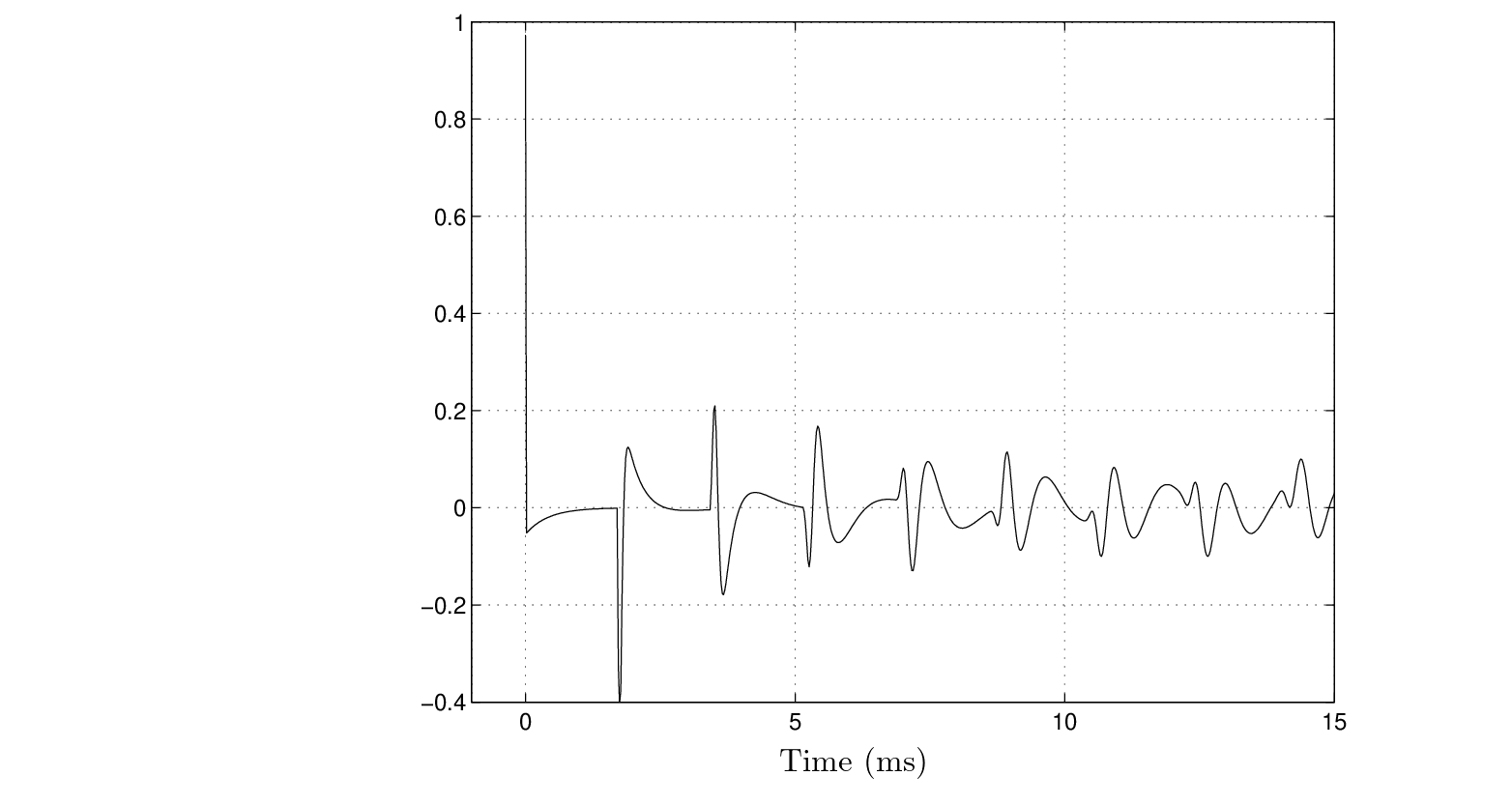
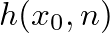 of a closed-open truncated cone is found from the digital waveguide structure of Fig. 7 as the pressure response at
of a closed-open truncated cone is found from the digital waveguide structure of Fig. 7 as the pressure response at 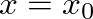 to the impulse response
to the impulse response
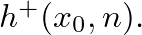
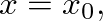 output scale factors are appropriately weighted by
output scale factors are appropriately weighted by 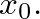
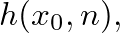 calculated using a Levine and Schwinger model of the open-end radiation and neglecting viscothermal losses.
calculated using a Levine and Schwinger model of the open-end radiation and neglecting viscothermal losses.
 |
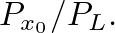

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |