Next: Modeling Approaches Up: Synthesizing Conical Instrument Sounds Previous: The Equivalent Circuit
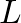 are shown to vary with respect to the parameter
are shown to vary with respect to the parameter 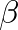 as depicted in Fig. 15.
as depicted in Fig. 15.
 |
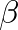 can be defined in terms of the ratio of input to output end radii,
can be defined in terms of the ratio of input to output end radii, 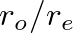 , or in terms of the ratio
, or in terms of the ratio
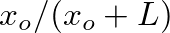 , where
, where 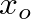 is the length of the missing, truncated apical section (see Fig. 13).
is the length of the missing, truncated apical section (see Fig. 13).
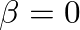 , while a closed-open cylinder is given by
, while a closed-open cylinder is given by 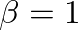 .
.
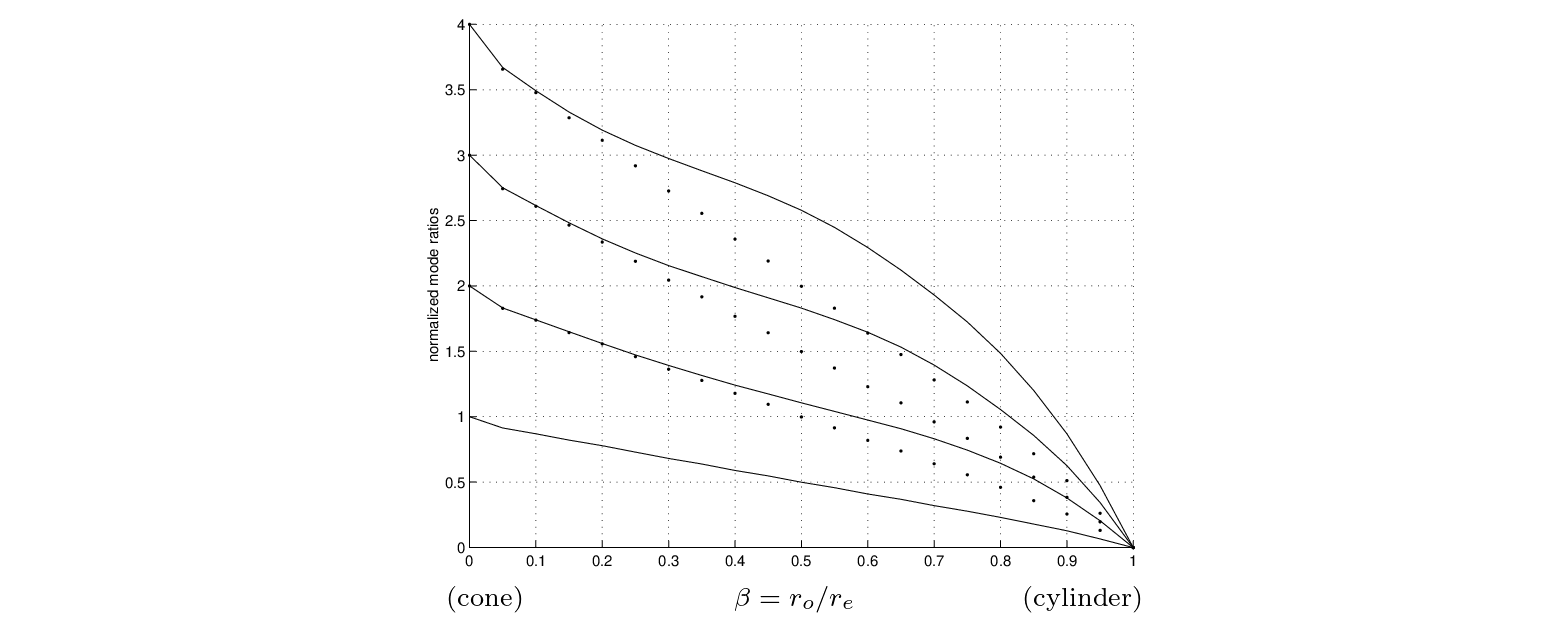 |
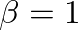 , the structure is of infinite length and all its modes converge to zero. In comparison with Fig. 15, the compound horn displays nearly harmonic mode ratios out to values of
, the structure is of infinite length and all its modes converge to zero. In comparison with Fig. 15, the compound horn displays nearly harmonic mode ratios out to values of 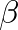 in the range 0.2–0.3.
in the range 0.2–0.3.
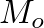 , in the equivalent circuit (Fig. 14). The inertance, whose magnitude varies with the parameter
, in the equivalent circuit (Fig. 14). The inertance, whose magnitude varies with the parameter 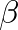 , tends to “shunt” low-frequency wave components, thus imposing a “high-pass” characteristic on the resulting air column mode structure.
, tends to “shunt” low-frequency wave components, thus imposing a “high-pass” characteristic on the resulting air column mode structure.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |