Next: Conical Bores: 1D Spherical Wave Up: Conical Air Column Acoustics Previous: Conical Air Column Acoustics
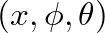 is depicted in Fig. 1. The wave equation in this geometric coordinate system is
is depicted in Fig. 1. The wave equation in this geometric coordinate system is
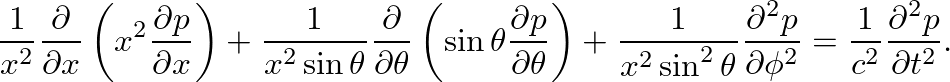 (1)
(1)
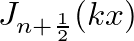 is a Bessel function and
is a Bessel function and
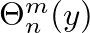 are associated Legendre functions.
are associated Legendre functions.
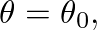 is
is
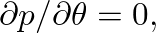 which can be met by adjusting the values of
which can be met by adjusting the values of 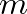 and
and 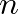 so that an extremum of
so that an extremum of
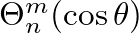 occurs at the wall.
occurs at the wall.
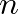 is nontrivial, and an accurate determination of cutoff frequencies for these modes is beyond the scope of this course. For axial symmetric waves (
is nontrivial, and an accurate determination of cutoff frequencies for these modes is beyond the scope of this course. For axial symmetric waves (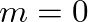 ), Hoersch (1925) has presented a method for determining values of
), Hoersch (1925) has presented a method for determining values of 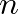 that satisfy the boundary condition in conical horns of various angles.
that satisfy the boundary condition in conical horns of various angles.
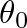 for saxophones, oboes, and bassoons are
for saxophones, oboes, and bassoons are 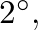
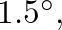 and
and 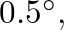 respectively (Nederveen, 1969). Using this procedure, the lowest values of
respectively (Nederveen, 1969). Using this procedure, the lowest values of 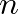 calculated for these angles are 109.27, 145.86, and 438.58, respectively.
calculated for these angles are 109.27, 145.86, and 438.58, respectively.
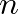 support these values and further indicate that solutions with
support these values and further indicate that solutions with 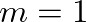 and
and 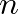 approximately equal to 53, 70, and 213, respectively are possible. These are nodal plane modes that correspond to the
approximately equal to 53, 70, and 213, respectively are possible. These are nodal plane modes that correspond to the 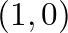 mode in cylinders. Cutoff frequencies for these values of
mode in cylinders. Cutoff frequencies for these values of 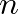 are determined where the expression
are determined where the expression
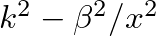 becomes positive.
becomes positive.
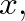 so that waves of sinusoidal type having
so that waves of sinusoidal type having 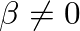 are only possible in the outer or wider portions of a cone (Benade and Jansson, 1974). Near the cone tip, any higher order modes that are excited will be evanescent.
are only possible in the outer or wider portions of a cone (Benade and Jansson, 1974). Near the cone tip, any higher order modes that are excited will be evanescent.
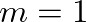 mode solutions given above, the corresponding cutoff frequencies are approximately
mode solutions given above, the corresponding cutoff frequencies are approximately 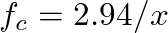 kHz for saxophones,
kHz for saxophones, 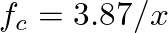 kHz for oboes, and
kHz for oboes, and 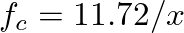 kHz for bassoons, where
kHz for bassoons, where 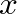 is given in meters.
is given in meters.
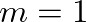 mode requires transverse circular motion, which will not occur with any regularity in musical instruments. As mentioned with regard to cylindrical bores, evanescent mode losses may occur in a woodwind instrument mouthpiece and near toneholes.
mode requires transverse circular motion, which will not occur with any regularity in musical instruments. As mentioned with regard to cylindrical bores, evanescent mode losses may occur in a woodwind instrument mouthpiece and near toneholes.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |