Next: Input Admittance of a Conical Up: Conical Air Column Acoustics Previous: Conical Bores: 1D Spherical Wave
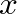 and frequency
and frequency 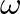 , sinusoidal pressure and volume velocity traveling-wave components are related by
with
, sinusoidal pressure and volume velocity traveling-wave components are related by
with
 (10)
(10)
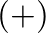 superscripts indicate wave components traveling in the positive
superscripts indicate wave components traveling in the positive 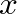 -direction or away from the cone apex, while negative
-direction or away from the cone apex, while negative 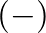 superscripts indicate travel in the negative
superscripts indicate travel in the negative 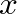 -direction or toward the apex.
-direction or toward the apex.
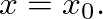 The frequency-domain pressure wave reflectance and transmittance for such a section, assuming a load impedance
The frequency-domain pressure wave reflectance and transmittance for such a section, assuming a load impedance 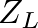 at
at 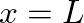 , are given by
and
, are given by
and
![$\displaystyle \frac{p(L,t)}{C^{+}} = \frac{e^{-jkL}}{L}\left[\frac{Z_{L} Z_{c}(L) + Z_{L} Z_{c}^{*}(L)}{Z_{L} Z_{c}(L) + Z_{c}(L) Z_{c}^{*}(L)}\right],
$](img65.png) (12)
(12)
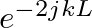 in Eq. (11) represents wave propagation to
in Eq. (11) represents wave propagation to 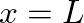 and back and has unity magnitude. The length parameter in this term is
and back and has unity magnitude. The length parameter in this term is 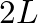 because the cone apex is defined at
because the cone apex is defined at 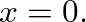
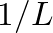 factor in the transmittance is characteristic of conical waveguides and results from the spreading of pressure across an increasing surface area as the traveling-wave component of pressure propagates away from the cone apex (Benade, 1988).
factor in the transmittance is characteristic of conical waveguides and results from the spreading of pressure across an increasing surface area as the traveling-wave component of pressure propagates away from the cone apex (Benade, 1988).
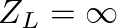 and taking the limit as
and taking the limit as
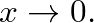 In this case, the term in brackets reduces to negative one.
In this case, the term in brackets reduces to negative one.
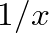 factors. The inversion of reflected pressure is necessary to maintain a finite pressure at
factors. The inversion of reflected pressure is necessary to maintain a finite pressure at 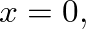 which can then be determined by l'Hôpital's rule (Ayers et al., 1985).
which can then be determined by l'Hôpital's rule (Ayers et al., 1985).
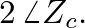 Since the angle of
Since the angle of 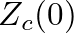 is
is 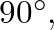 pressure is reflected from the tip with a
pressure is reflected from the tip with a 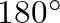 phase shift or with an inversion.
phase shift or with an inversion.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |