Next: Conical Air Column Modeling Up: Conical Air Column Acoustics Previous: Input Admittance of a Conical
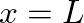 is ideally open, so that
is ideally open, so that 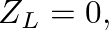 the reflectance
the reflectance 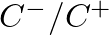 becomes
becomes 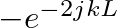 and the input admittance of a truncated cone reduces to
where
and the input admittance of a truncated cone reduces to
where
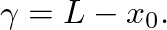
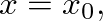 is assumed ideally open, the resonance frequencies of the open-open (o-o) conic frustum are at the infinities of Eq. (16), which are given for
is assumed ideally open, the resonance frequencies of the open-open (o-o) conic frustum are at the infinities of Eq. (16), which are given for
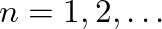 by
by
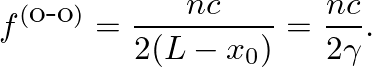 (17)
(17)
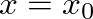 is assumed ideally closed, which is nearly the case for reed-driven conical woodwind instruments, the resonance frequencies are found at the zeros of the input admittance.
is assumed ideally closed, which is nearly the case for reed-driven conical woodwind instruments, the resonance frequencies are found at the zeros of the input admittance.
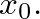
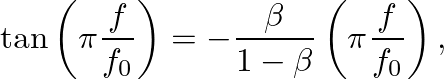 (19)
(19)
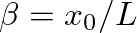 and
and
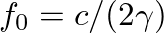 is the fundamental frequency for the open-open conic frustum of length
is the fundamental frequency for the open-open conic frustum of length 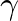 (Ayers et al., 1985).
(Ayers et al., 1985).
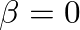 (complete cone) to
(complete cone) to 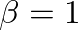 (closed-open cylinder).
(closed-open cylinder).
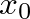 but decreases with frequency. Viewed in terms of the normal modes of a closed-open cylinder, however, the inertance contributes a negative length correction that is inversely proportional to truncation
but decreases with frequency. Viewed in terms of the normal modes of a closed-open cylinder, however, the inertance contributes a negative length correction that is inversely proportional to truncation 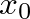 and frequency.
and frequency.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |