Next: Reflection at a Rigid Boundary Up: Conical Air Column Modeling Previous: Conical Air Column Modeling
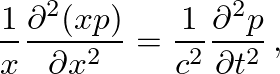 (20)
(20)
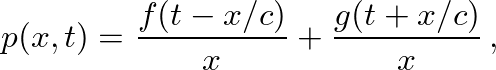 (21)
(21)
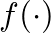 and
and 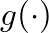 are completely general and continuous and can be interpreted as arbitrarily fixed waveshapes that travel in opposite directions along the
are completely general and continuous and can be interpreted as arbitrarily fixed waveshapes that travel in opposite directions along the 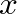 -axis with speed
-axis with speed 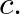
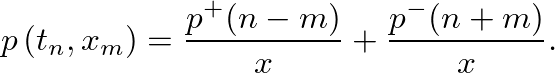 (22)
(22)
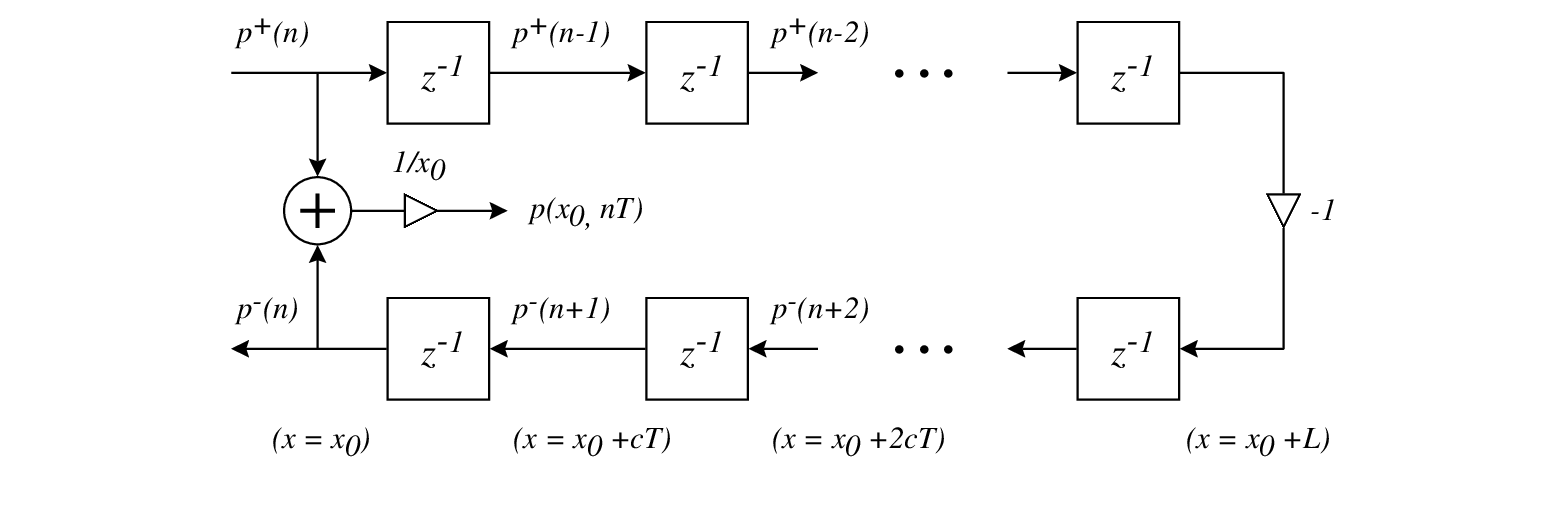 |
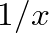 scale factors, which are implemented at observation points, the cylindrical and conical waveguide implementations are exactly the same.
scale factors, which are implemented at observation points, the cylindrical and conical waveguide implementations are exactly the same.
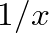 scale factor is unnecessary.
scale factor is unnecessary.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |