Next: Impulse Response Up: Cylindrical Air Column Modeling Previous: An Ideal Digital Waveguide Model
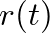
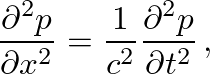 Thermal and viscous boundary layer losses are neglected in this model.
Thermal and viscous boundary layer losses are neglected in this model.
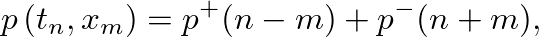 |
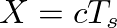 can be “pushed” through the lower delay line to its output and a single delay line used for the simulation, as shown in Fig. 10.
can be “pushed” through the lower delay line to its output and a single delay line used for the simulation, as shown in Fig. 10.
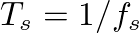 |

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |