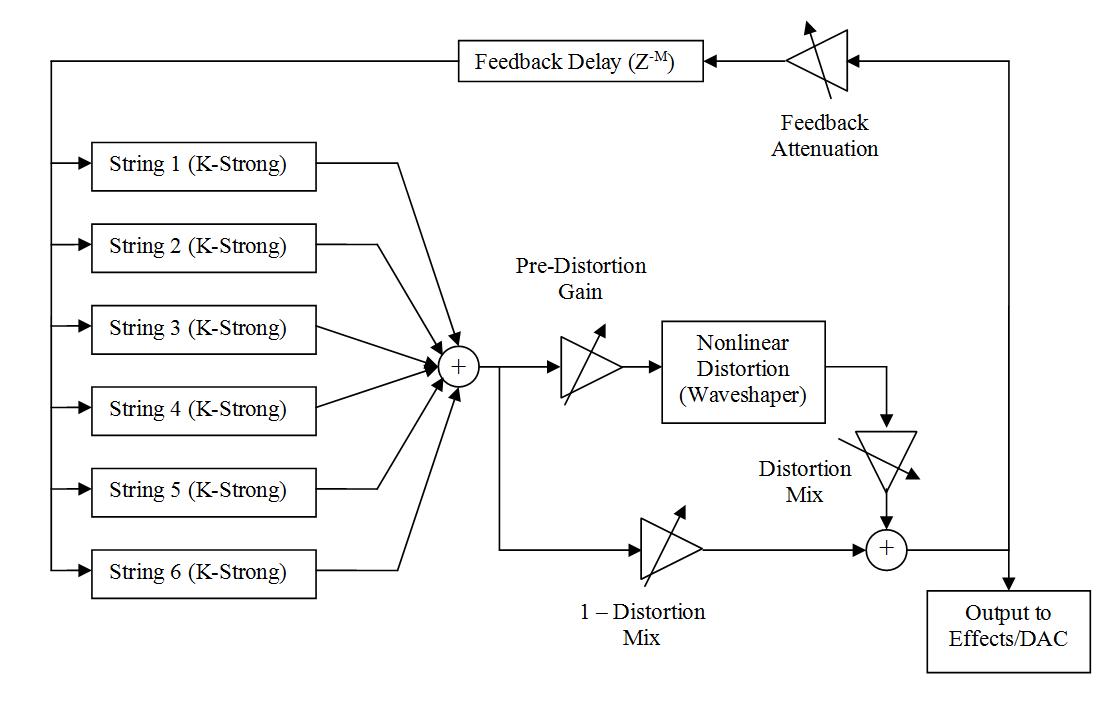
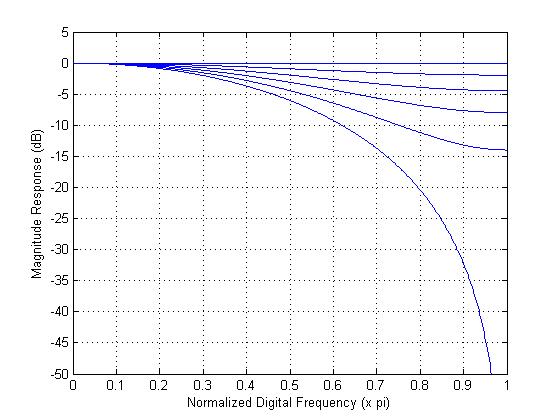
Figure 1: Synthesis Model Block Diagram
An Electric Guitar Plucked String Model for
Realtime Control with Distortion and Feedback
| The Karplus-Strong plucked string algorithm, originally published in 1983 (Karplus, Strong 1983) and improved that same year (Jaffe, Smith 1983), provides a simple and computationally efficient method for synthesizing plucked string-like sounds. Methods have been explored for extending this algorithm to simulate the timbre of particular instruments, such as the amplified and distorted electric guitar (Sullivan, 1990). This purpose of this project is to implement a real-time electric guitar synthesis model using many of the extensions proposed by Sullivan, as well as to explore improvements to these extensions and develop a parameterizable control scheme for the synthesis model. |

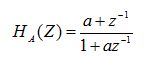
 samples, the coefficient a is given by:
samples, the coefficient a is given by: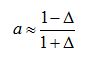
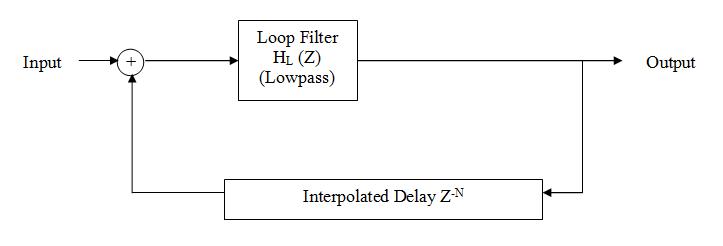
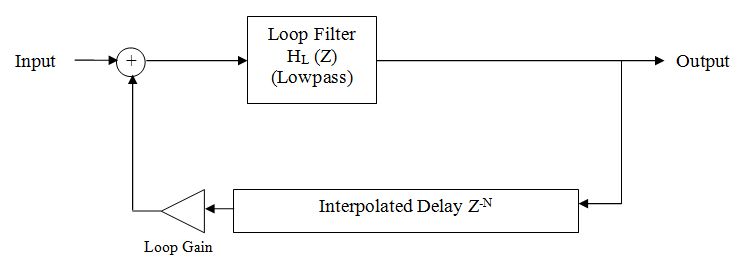
 samples, this filter has a transfer function given by:
samples, this filter has a transfer function given by: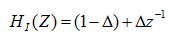
 results in a smooth and continuous change in the delay line length, because setting
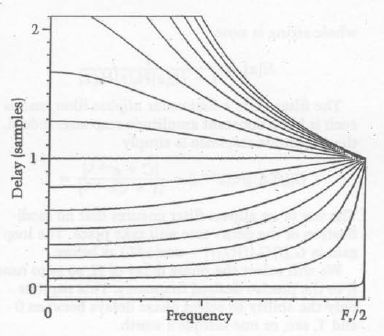
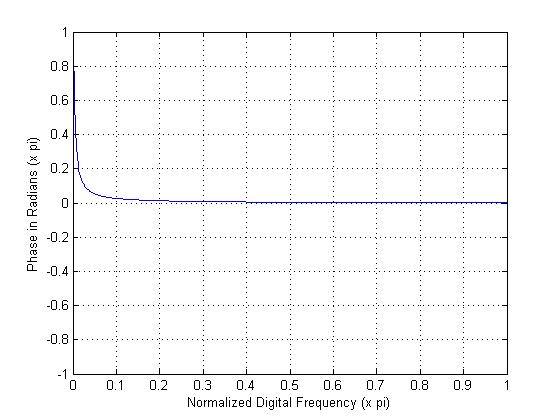
results in a smooth and continuous change in the delay line length, because setting  = 1 is equivalent to simply extending the delay line by one sample. This is not the case in the allpass filter, where care must be taken to ensure that the coefficient is within an acceptable range of values for near-linear phase response (
= 1 is equivalent to simply extending the delay line by one sample. This is not the case in the allpass filter, where care must be taken to ensure that the coefficient is within an acceptable range of values for near-linear phase response ( between 0.3-1.3). In the case of smooth delay line length changes, as in pitch bends, he suggests that this would result in audible "clicks" when the coefficient must suddenly jump down or up to satisfy this threshold.
between 0.3-1.3). In the case of smooth delay line length changes, as in pitch bends, he suggests that this would result in audible "clicks" when the coefficient must suddenly jump down or up to satisfy this threshold. (Figure 4). Take for example the case where
(Figure 4). Take for example the case where  = 0.5, and we have a transfer function identical to the original Karplus Strong loop filter. In this case, and any case for
= 0.5, and we have a transfer function identical to the original Karplus Strong loop filter. In this case, and any case for  not equal to zero or one, the interpolating filter is lowpass in character, which means that the higher frequencies in the plucked string signal will be attenuated depending on the desired delay line length.
not equal to zero or one, the interpolating filter is lowpass in character, which means that the higher frequencies in the plucked string signal will be attenuated depending on the desired delay line length.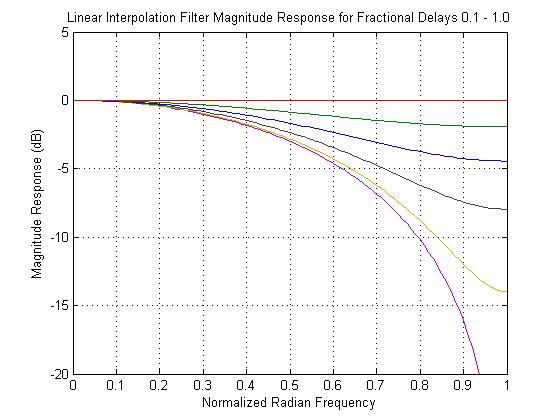
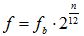
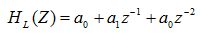
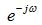 :
: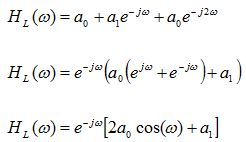
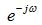 is equivalent to a unit delay in the discrete-time domain, the approximate delay through the filter is constant and equal to 1 sample over all frequencies, which should be subtracted from the delay line length to preserve precise tuning.
is equivalent to a unit delay in the discrete-time domain, the approximate delay through the filter is constant and equal to 1 sample over all frequencies, which should be subtracted from the delay line length to preserve precise tuning.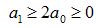
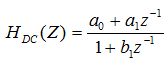
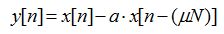
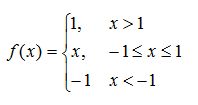
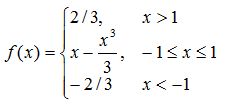
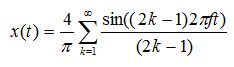
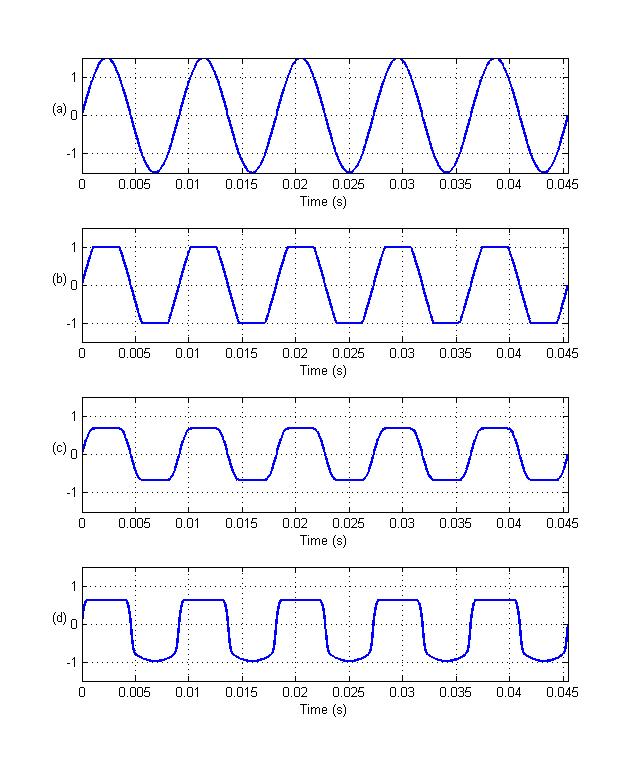
| MIDI Control Number | Function |
| Pitch Bend Wheel | Bend/Whammy |
| Modulation Wheel (1) | Vibrato Amplitude |
| 21 | Main Volume (Post Feedback) |
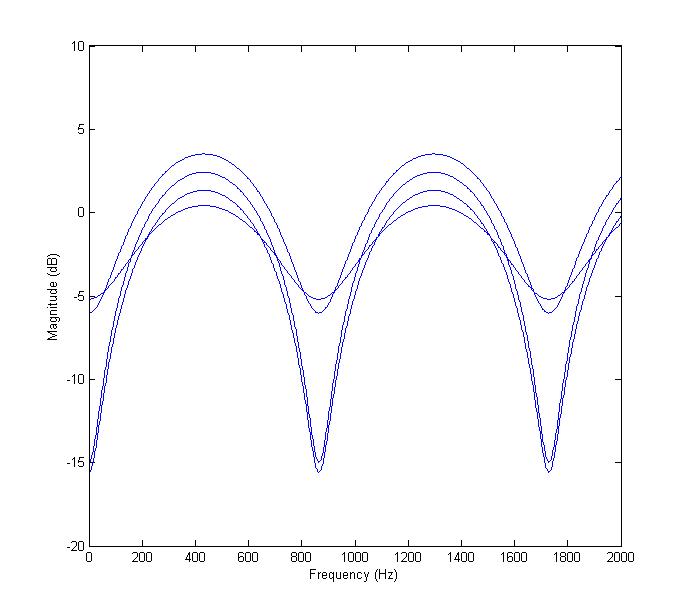
| 22 | Loop Filter Control (harmonic decay rate) |
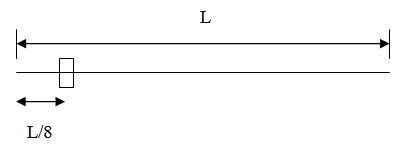
| 23 | Pickup Position |
| 24 | Pickup Mix |
| 27 | Feedback Delay Time |
| 28 | Feedback Attenuation |
| 70 | Distortion Type |
| 71 | Pre-Distortion Gain |
| 72 | Distortion Mix |
| 73 | Loop Decay |
| 91 | Sustain Level (damping) |
| 93 | Delay Effect Delay Time |
| 82 | Delay Effect Feedback |
| 83 | Delay Effect Mix |