MUMT 307

Outline

  • Convolution
  • Reverb
  • Reverb (lab)
  • Audio File Formats
  • Wavetable ann Additive Synthesis
  • Wavetable ann Additive Synthesis (lab)
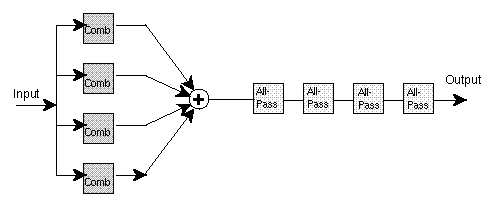
Traditional reverb (Schroeder's)
Schroeder's
source: https://ccrma.stanford.edu/software/clm/compmus/clm-tutorials/processing2.html#rev
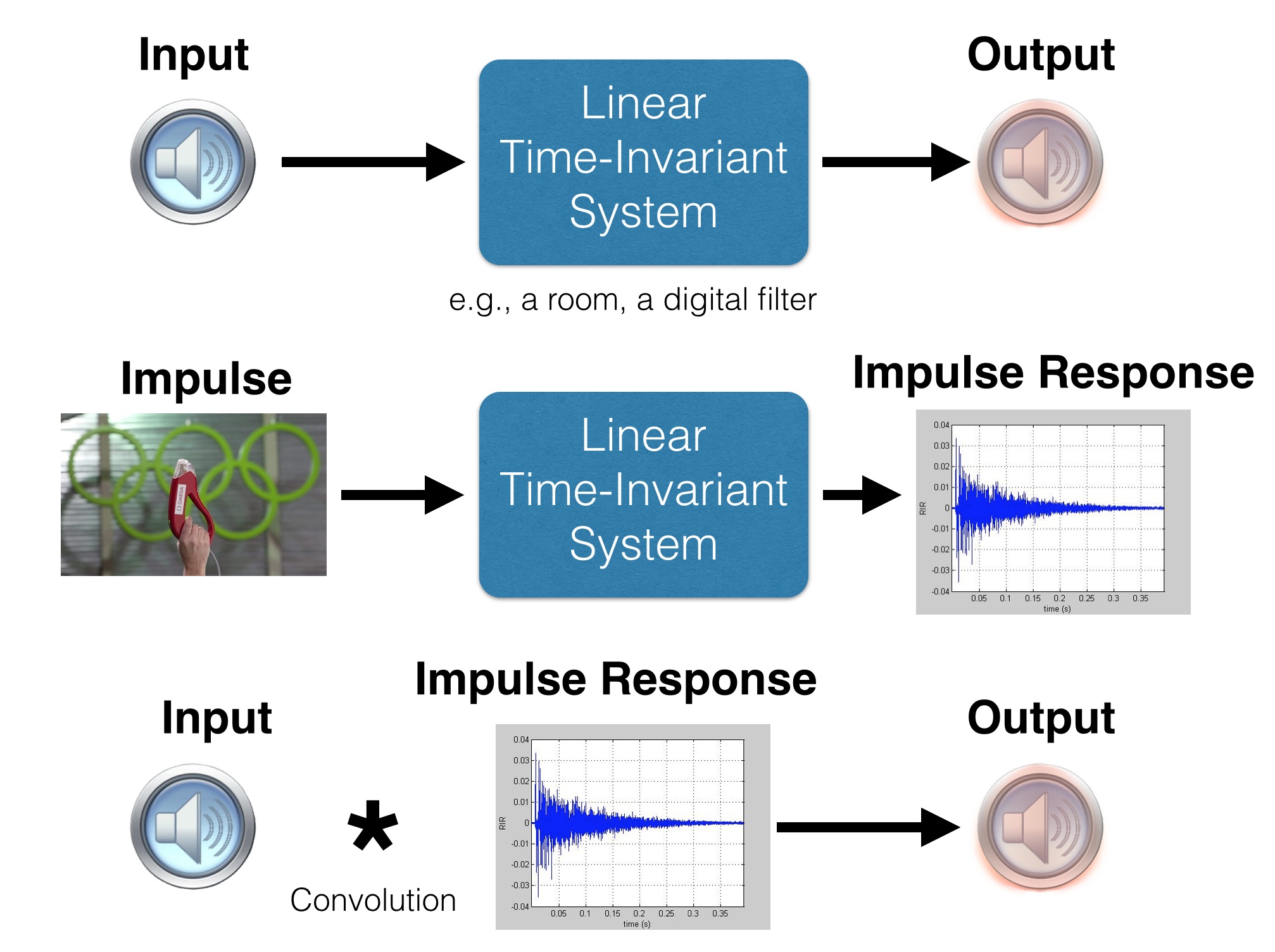
Convolution
LTI System

MUMT 307

Reverb

Convolution 1
An impulse function: `delta(n)={(1, n=0), (0, otherwise):}`
`x(n)=sum_(k=-oo)^oox(k)delta(n-k)`

A system (a transform): `y(n)=T[x(n)]`

`y(n)=T[sum_(k=-oo)^oox(k)delta(n-k)]`

If `T` is linear:
(i.e., `T[alpha f(n)+beta g(n)] = alpha T[f(n)]+beta T[g(n)]`)
`y(n)=sum_(k=-oo)^oox(k)T[delta(n-k)]`
Convolution 2
Assuming `T` is linear:
`y(n)=sum_(k=-oo)^oox(k)T[delta(n-k)]`
If `T` is also time invariant:
`y(n) = T[x(n)] -> y(n-k) = T[x(n-k)]`
If `h(n)` is a response of `T` to `delta(n)` then:
`h(n) = T[delta(n)] -> h(n-k) = T[delta(n-k)]`
`y(n)=sum_(k=-oo)^oox(k)h(n-k)`
But `h(n)` is the impulse reponse of `T`
Convolution 3
This is the definition of convolution:
`y(n)=sum_(k=-oo)^oox(k)h(n-k)`
Also noted as: `y(n) = x(n)` * `h(n)`
The relationship with corss-corrleation

Fast Convolution
`y(n) = IFT{FT[x(n)] * FT[h(n)]}`
The convolution is the same as the inverse Fourier transoform of the multiplication of the input and the impulse response in the frequency domain!

MUMT 307

Reverb 1 (lab)

MUMT 307

Reverb 2 (lab)

MUMT 307

Audio File Format

  • List of different audio file formats
  • Compressed vs Uncompressed
    • Why compress?
    • How much can it be compressed?
    • Lossless vs Lossy
    • When do you not want to compress, even lossless?
    • Sound quality
    • Metadata
    • Open vs Proprietry technologies
  • Containers
  • DRM

MUMT 307

Uncompressed (lossless) audio file format

  • Bit width: 16-24 bits
  • Sampling rates: 44.1kHz, 48kHz, 96kHz, 192kHz
  • PCM (header less): Pulse-coded Modulation
  • AIFF (Audio Interchange File Format)
  • WAVE & WAVE BWF

MUMT 307

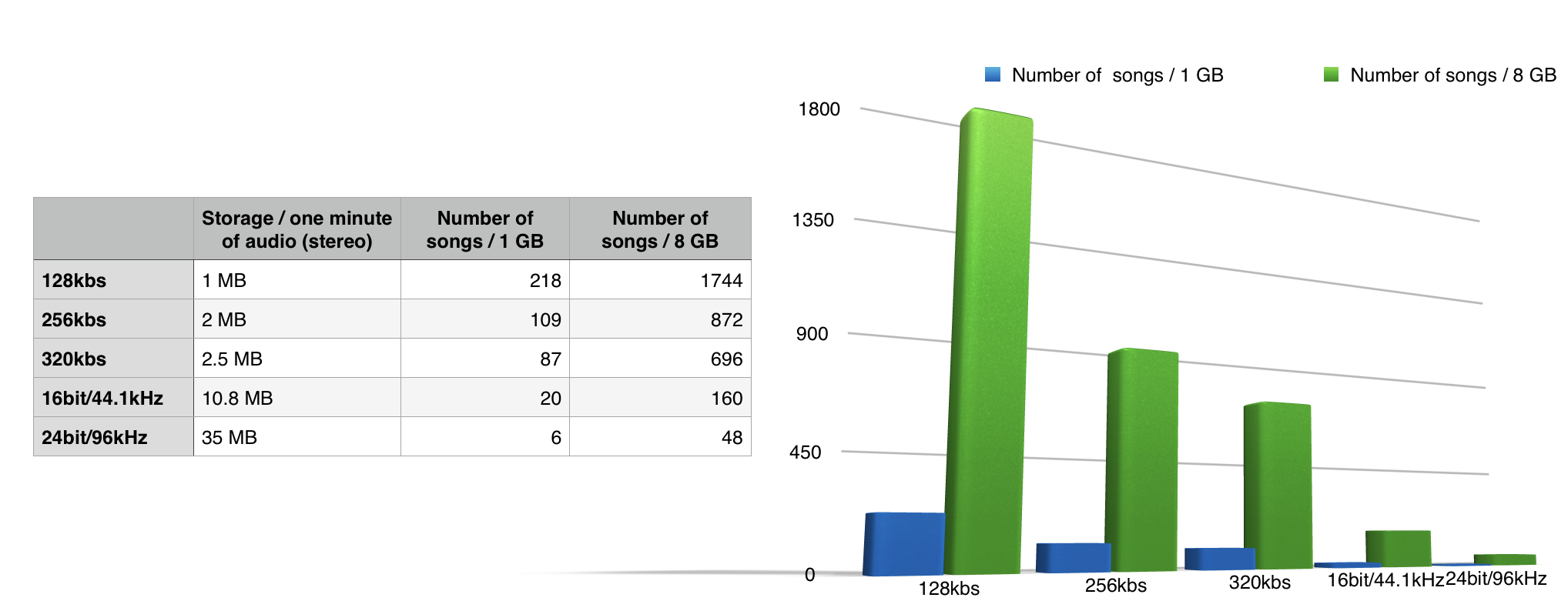
Audio file size

MUMT 307

Compressed audio file format

  • Lossless (typically 2:1)
    • FLAC (Free Lossless Audio Codec)
    • WMA Lossless
  • Lossy (up to 10:1 or more)
    • MP3: MPEG I/II Layer 3
    • Ogg Vorbis
    • WMA
    • AAC

MUMT 307

Lossy Perceptual Audio Coding

  • MP3 (MPEG I/II Layer III)
    • Karlheinz Brandenburg
    • Stereo or 5.1 channels
    • Sampling frequency: 16-48kHz
  • AAC (Advanced Audio Coding; 1997)
    • m4a: created by iTUnes when importing from CDs
    • m4p (DRM protected): when you buy a song from Apple on iTunes (as of 2009/01, iTunes offer DRM-free songs)
    • Up to 48 channels
    • Sampling frequency: 8–96kHz
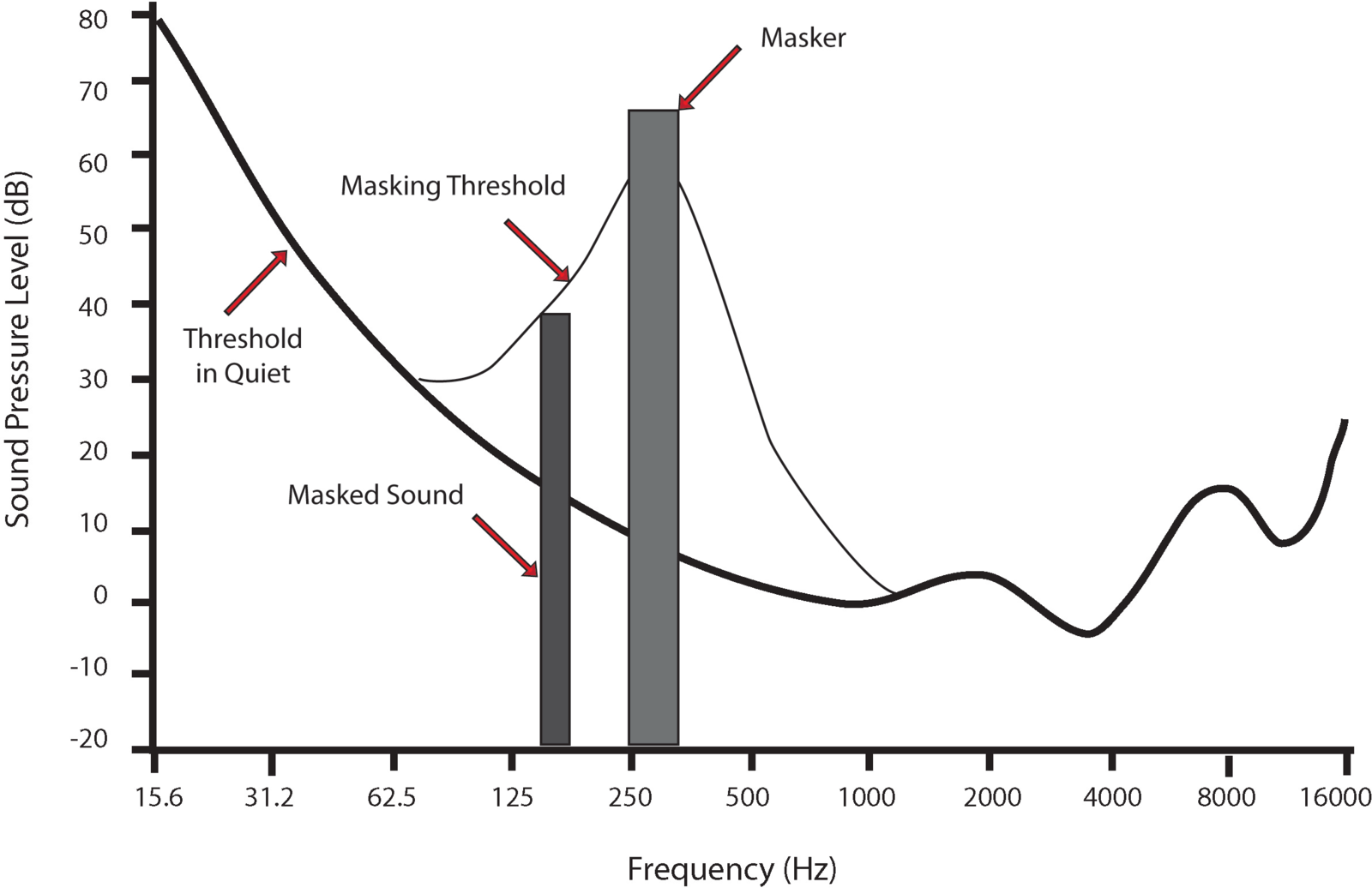
Audio Masking
Audio Masking
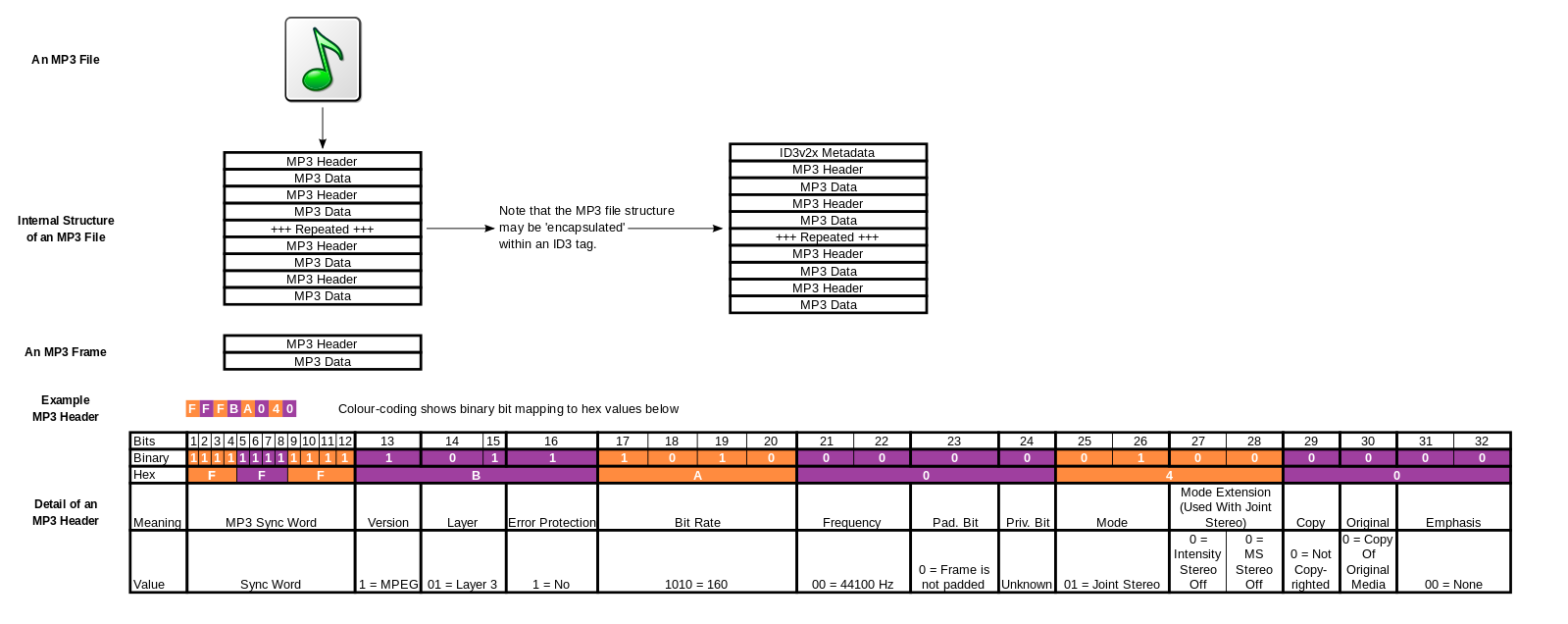
MP3 File Structure

MUMT 307

Containers

  • Audio only
    • AIFF (Apple 1989)
    • WAV (Microsoft & IBM 1991)
  • General (multimedia)
    • Matroska
    • Ogg
    • MPEG: MP4
    • AVI
    • AES-31
    • METS

MUMT 307

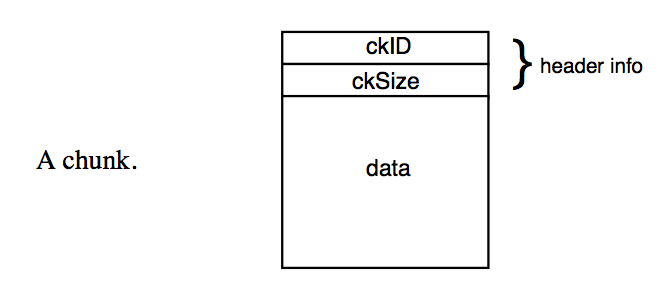
IFF File Format

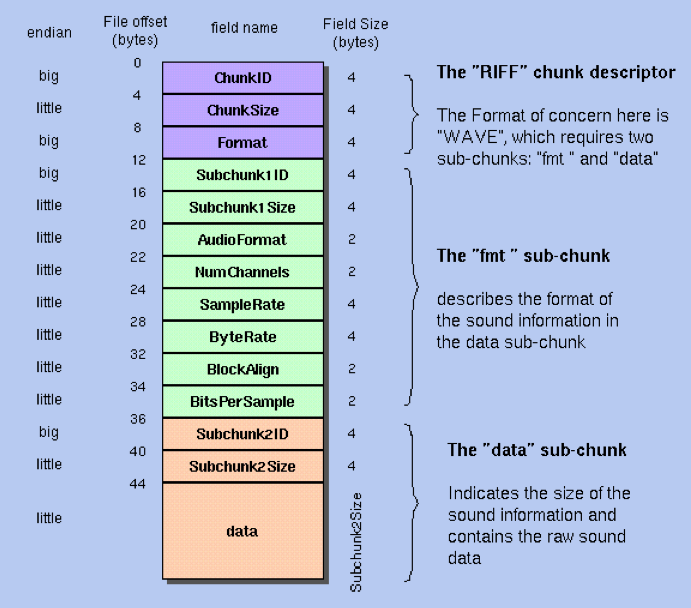
  • Interchange File Format: AIFF (big-endian), RIFF (little-endian), WAV (not TIFF)
  • Based on "EA IFF 85"
  • Based on "chunks"
  • Extensible
IFF file format

WAV File Format

WAV File Format

Little endian vs Big endian

Little endian vs Big endian

MUMT 307

Lossy vs Lossless

  • Q: Can people hear the difference?
  • A: It depends
  • Listeners can tell the difference between CD quality and MP3 compression (92–192 kb/s) [Amandine et al. 2009]
  • Listeners can not tell the difference between CD quality and MP3 compression (256–320 kb/s) [Amandine et al. 2009]
  • Listening test

MUMT 307

Wavetable and Additive Synthesis

MUMT 307

Wavetable and Additive Synthesis (lab)

  • Using the PeriodicWave demo, create a sawtooth wavetable and a triangular wavetable with the following Fourier series with the fundamental frequency `f` (lab):
    • Square: `4/pisum_(k=0)^oo 1/k sin(2pifkt) text{ for } k=1,3,5,...`
    Sawtooth: `1/2 - 1/pisum_(k=0)^oo 1/k sin(2pifkt) text{ for } k=1,2,3,...`
    Square: `8/pi^2sum_(k=0)^oo (-1)^{(k-1)//2}/k^2 sin(2pifkt) text{ for } k=1,3,5,...`