Next: Why does the KS Algorithm Up: Physical Modeling Previous: Physical Modeling Approaches for Sound
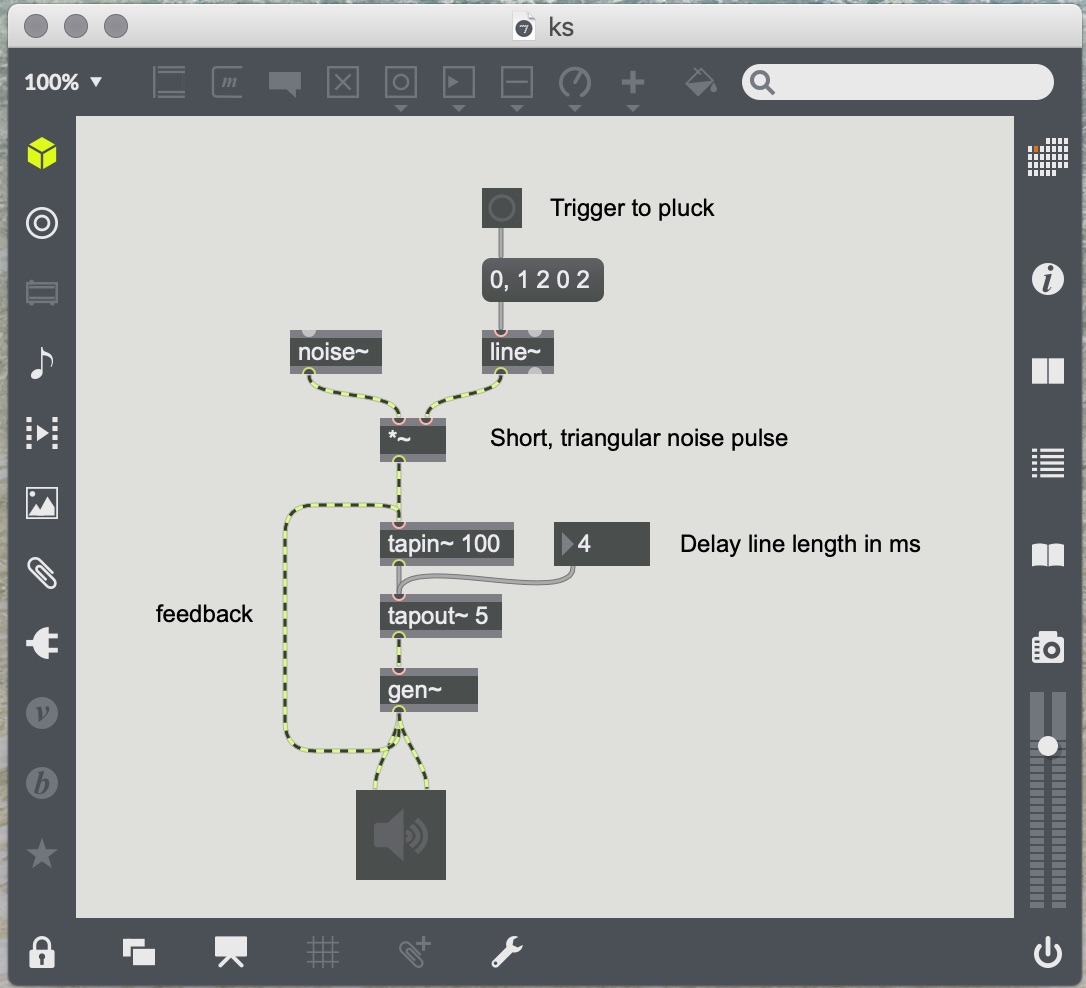
![$y[n] = 0.5 x[n] + 0.5 x[n-1]$](img56.png) . The wavetable is initialized with psuedo-random numbers.
. The wavetable is initialized with psuedo-random numbers.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |