Next: Lossy Wave Propagation Up: Physical Modeling Previous: Why does the KS Algorithm
In the same way they can be used to simulate traveling waves in free space (our first simple physical model), delay lines can be used to simulate one-dimensional (1D) wave propagation along strings or in acoustic tubes. Since waves can propagate simultaneously in two opposite directions along a 1D waveguide, two delay lines are necessary (wave simulation, waves on a string).
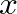 axis (such as a stretched string) is described mathematically by the one-dimension wave equation as:
axis (such as a stretched string) is described mathematically by the one-dimension wave equation as:
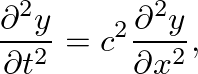
 is the direction perpendicular to the
is the direction perpendicular to the 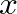 axis and
axis and 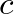 is the speed of wave motion in the medium.
is the speed of wave motion in the medium.
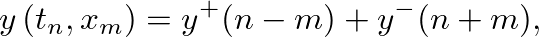 (3)
(3)
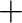 and
and  denote wave components travelling to the right and left, respectively, with time indices
denote wave components travelling to the right and left, respectively, with time indices 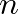 and spatial indices
and spatial indices 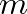 .
.
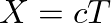 meters, or the distance traveled by a wave in one temporal sampling interval. In this way, each traveling-wave component moves left or right one spatial sample for each time sample.
meters, or the distance traveled by a wave in one temporal sampling interval. In this way, each traveling-wave component moves left or right one spatial sample for each time sample.
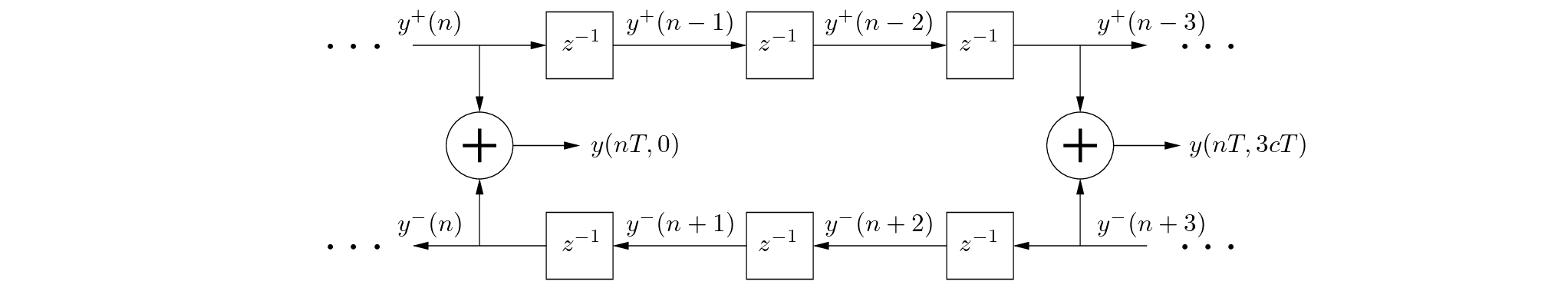 |

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |