Next: An Acoustic Correlate: The Helmoltz Up: Modal Synthesis Previous: Modal Synthesis
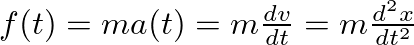
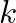 .
.
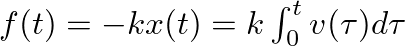 for
for 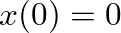 (valid for small, non-distorting displacements)
(valid for small, non-distorting displacements)
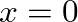 . A positive value of
. A positive value of 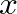 produces a negative restoring force.
produces a negative restoring force.
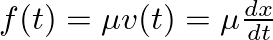
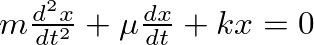
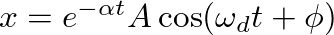 , where
, where
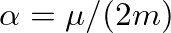 is a decay constant and
is a decay constant and
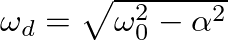 is the characteristic (or natural) angular frequency of the system.
is the characteristic (or natural) angular frequency of the system.
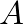 and
and 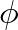 are determined by the initial displacement and velocity.
are determined by the initial displacement and velocity.
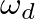 is lower than that of the mass-spring system (without damping) (
is lower than that of the mass-spring system (without damping) (
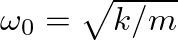 ).
).

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |