Next: Parameter Estimation Up: Modal Synthesis Previous: An Acoustic Correlate: The Helmoltz
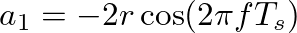
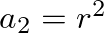
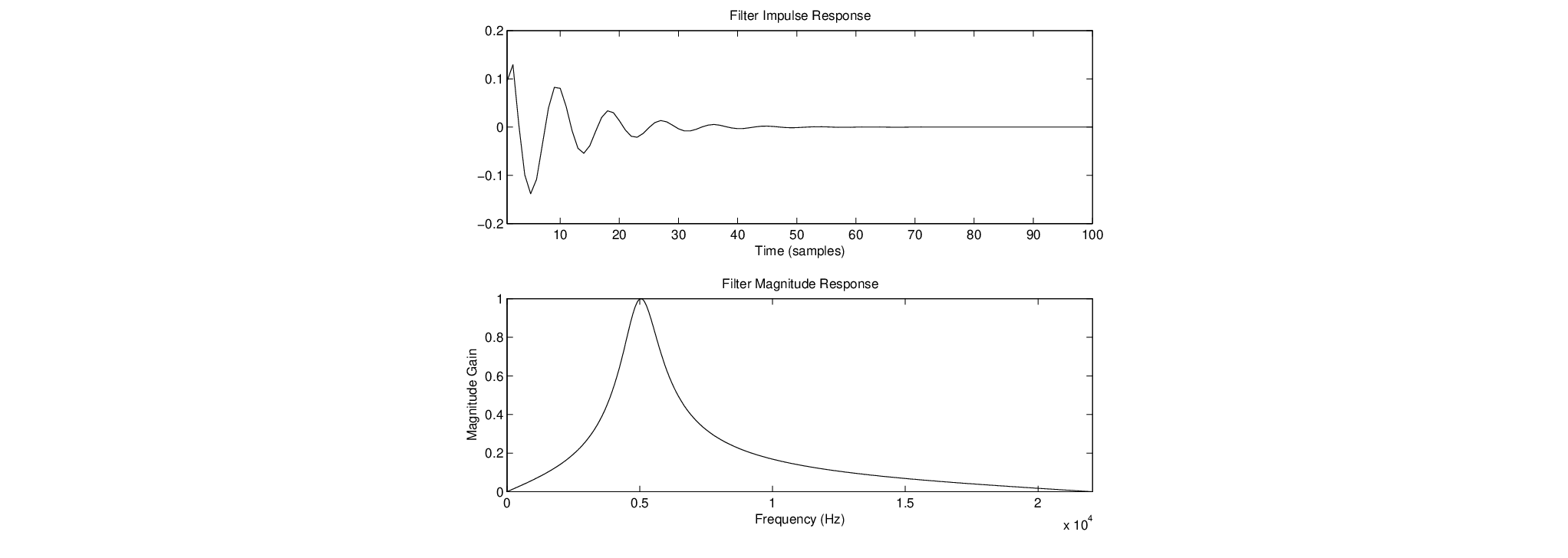
where 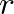 is a value between 0 – 1.0 that sets the pole radius and
is a value between 0 – 1.0 that sets the pole radius and 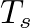 is the sample period.
is the sample period.
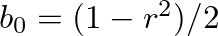
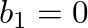
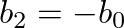
 |

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |