Next: Another Simple Physical Model Up: Physical Modeling Previous: What is a Physical Model?
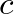 = 345 meters / second in air.
= 345 meters / second in air.
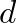 thus involves a time delay of
thus involves a time delay of 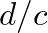 seconds.
seconds.
![$\displaystyle y[n] = x[n - M], \hspace{0.2in} n = 0, 1, 2, \ldots,
$](img44.png)
![$x[n] \ensuremath{\stackrel{\Delta}{=}}0$](img45.png) for
for 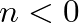 ,
, ![$y[n]$](img47.png) is the output signal and
is the output signal and 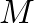 is the delay length in samples.
is the delay length in samples.
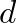 , where
, where
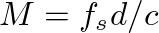 is the number of discrete-time samples corresponding to a distance
is the number of discrete-time samples corresponding to a distance 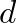 at a sample rate
at a sample rate 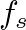 .
.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |