Next: Windowing Up: The Short-Time Fourier Transform Previous: The Short-Time Fourier Transform
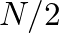 . Thus, the larger
. Thus, the larger 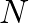 , the more sinusoids will be available for comparison and the smaller the “cracks” between DFT components.
, the more sinusoids will be available for comparison and the smaller the “cracks” between DFT components.
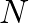 “average out” time variations in the signal. If the frequency content of a signal is changing relatively quickly in time, the only way these variations can be identified is by using small values of
“average out” time variations in the signal. If the frequency content of a signal is changing relatively quickly in time, the only way these variations can be identified is by using small values of 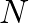 .
.
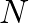 samples and an FFT is computed for each section.
samples and an FFT is computed for each section.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |