Up: Parameter Estimation Previous: Center Frequencies: Parabolic Interpolation
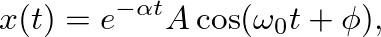 (17)
(17)
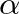 is a decay constant,
is a decay constant, 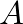 is the amplitude,
is the amplitude, 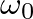 is the natural radian frequency and
is the natural radian frequency and 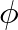 is a phase offset.
is a phase offset.
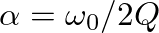 .
.
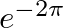 from its original energy and is commonly defined as
from its original energy and is commonly defined as
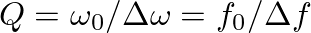 , where the bandwidth
, where the bandwidth 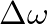 (or
(or 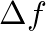 ) is the range of frequencies (in radians or Hertz) for which the energy is at least half its peak amplitude.
) is the range of frequencies (in radians or Hertz) for which the energy is at least half its peak amplitude.
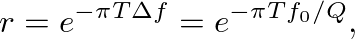 (18)
(18)
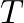 is the sample period.
is the sample period.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |