Next: A Discrete-Time Sinusoidal Signal Up: Spectral Analysis Previous: Spectral Analysis
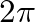 radians), they naturally represent periodic signals. On the other hand, one should expect that any attempt to decompose a non-periodic signal into sinusoidal components will have limitations.
radians), they naturally represent periodic signals. On the other hand, one should expect that any attempt to decompose a non-periodic signal into sinusoidal components will have limitations.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |