Next: Sum of Sinusoids using Complex Up: Complex Exponential Signals Previous: Complex Exponential Signals
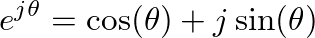
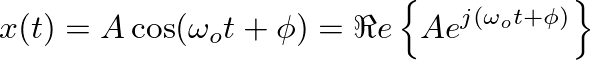
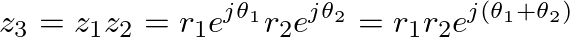
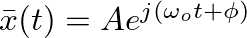 can be rewritten
can be rewritten
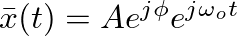 .
.
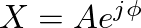 as the complex amplitude (the time-invariant part), polar representation of amplitude and phase shift of the complex exponential signal. This term also represents a vector in the complex plane where
as the complex amplitude (the time-invariant part), polar representation of amplitude and phase shift of the complex exponential signal. This term also represents a vector in the complex plane where 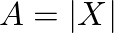 and
and
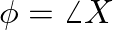 .
.
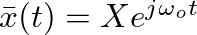 . The
. The
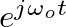 term has magnitude = 1 and can be interpreted as adding an incremental angle or phase shift to
term has magnitude = 1 and can be interpreted as adding an incremental angle or phase shift to 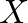 every time step
every time step 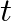 .
.
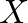 is a phasor rotating in the complex plane with radian frequency
is a phasor rotating in the complex plane with radian frequency
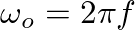 .
.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |