Next: Dispersion Up: Multi-Dimensional Modeling Previous: A Rectilinear Two-Dimensional Plate Model
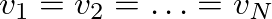
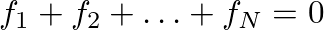
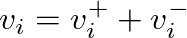 and
and
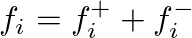 , are related by their respective port wave impedances:
, are related by their respective port wave impedances:
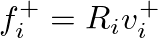 and
and
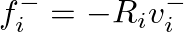 .
.
 -port junction can be derived:
-port junction can be derived:
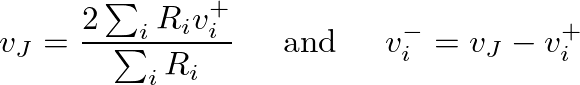
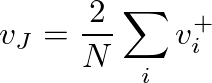
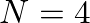 ) junction, the scale factor
) junction, the scale factor 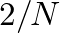 reduces to
reduces to 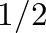 , which can be implemented in fixed-point arithmetic with a bit shift.
, which can be implemented in fixed-point arithmetic with a bit shift.
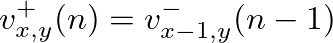
![$\displaystyle u_{tt}(t,x,y) = c^{2} [ u_{xx}(t,x,y) + u_{yy}(t,x,y) ],
$](img16.png)
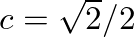 and the time and spatial sampling intervals (
and the time and spatial sampling intervals (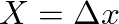 ,
, 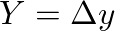 ,
, 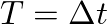 ) all equal to one another.
) all equal to one another.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |