Next: Doppler Effect Up: Delay-Based Effects Previous: Delay-Based Effects
![$\displaystyle y[n] = x[n] + g x[n - M[n]],
$](img31.png)
![$M[n]$](img32.png) is the time-varying length of a delay line and
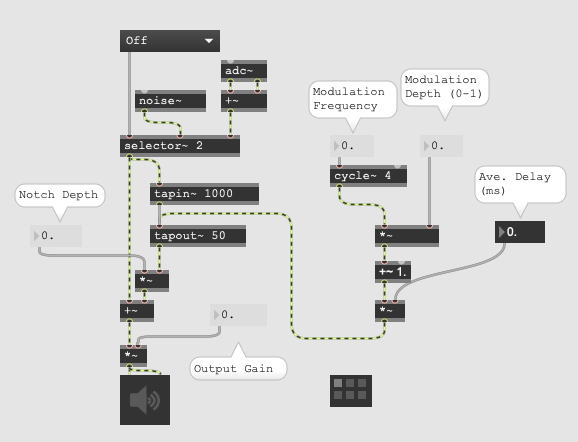
is the time-varying length of a delay line and 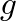 is the “depth” of the flanging effect. A flanger block diagram is shown in Fig. 6.
is the “depth” of the flanging effect. A flanger block diagram is shown in Fig. 6.
![$M[n]$](img32.png) , must change continuously and smoothly through time, it is necessary to make use of an interpolating delay line.
, must change continuously and smoothly through time, it is necessary to make use of an interpolating delay line.
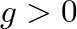 , there are
, there are 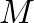 peaks in the frequency response, centered about the frequencies
peaks in the frequency response, centered about the frequencies
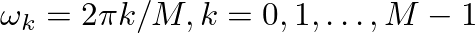 . Between these peaks, there are
. Between these peaks, there are 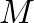 notches at intervals of
notches at intervals of 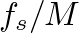 Hz.
Hz.
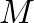 changes over time, the peaks and notches of the comb response are compressed and expanded. The spectrum of a sound passing through the flanger is thus accentuated and deaccentuated by frequency region in a time-varying manner.
changes over time, the peaks and notches of the comb response are compressed and expanded. The spectrum of a sound passing through the flanger is thus accentuated and deaccentuated by frequency region in a time-varying manner.
![$\displaystyle M[n] = M_{0} \cdot (1 + A \sin[2 \pi f n T_s]),
$](img40.png)
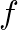 is the flanger “rate” in Hz,
is the flanger “rate” in Hz, 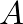 is the “excursion” (maximum delay swing),
is the “excursion” (maximum delay swing), 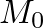 is the average delay-line length that controls the average notch density, and
is the average delay-line length that controls the average notch density, and 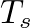 is the sample period.
is the sample period.
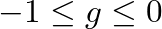 , the peaks and notches of the comb filter trade places. In practice,
, the peaks and notches of the comb filter trade places. In practice, 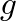 is normally contrained to the interval
is normally contrained to the interval ![$[0,1]$](img45.png) and the option of sign inversion is provided by a “phase inversion” switch.
and the option of sign inversion is provided by a “phase inversion” switch.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |