Next: Boundary Conditions Up: Digital Waveguide Theory Previous: Lossy Wave Propagation
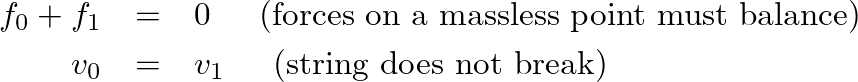
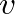 denote the common transverse velocity of the string at the junction. Then the traveling-wave components of velocity can be written
denote the common transverse velocity of the string at the junction. Then the traveling-wave components of velocity can be written
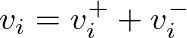 or
or
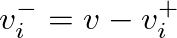 .
.
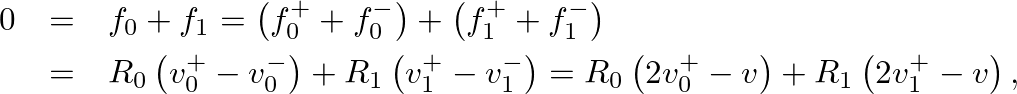
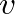 as
as
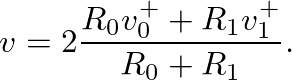
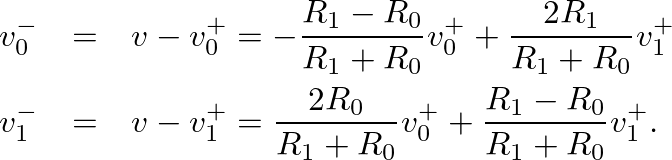
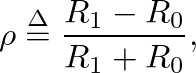
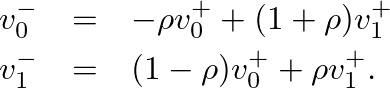
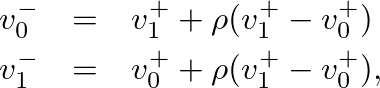

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |