Next: Simulating Pluck/Strike Position Up: String Modeling Previous: The Ideal Struck String
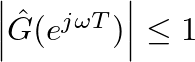 .
.
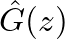 representing losses and inversion at the bridge, and an inversion representing reflection from the nut, as shown below. Additional simplifications are possible.
representing losses and inversion at the bridge, and an inversion representing reflection from the nut, as shown below. Additional simplifications are possible.
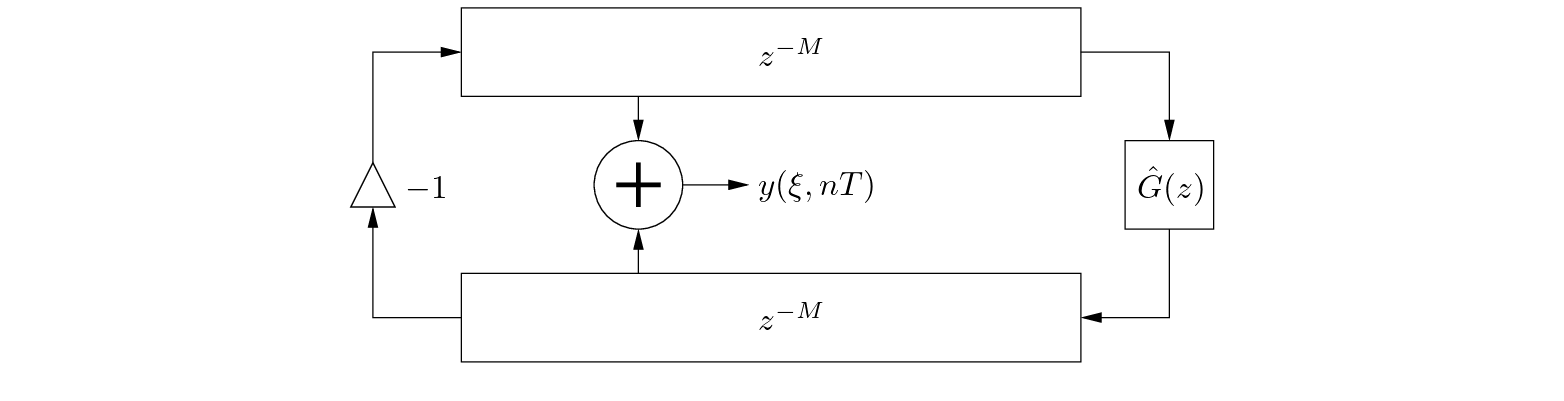 |

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |