Next: Finite Length Cylindrical Pipes Up: Cylindrical Air Column Acoustics Previous: Cylindrical Pipes: Modes of Propagation
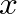 -axis with sinusoidal time dependence has the form
which is a solution to the one-dimensional wave equation
-axis with sinusoidal time dependence has the form
which is a solution to the one-dimensional wave equation
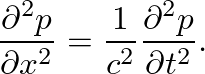 (18)
(18)
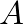 is the cross-sectional area of the pipe and
is the cross-sectional area of the pipe and 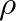 is the mass density of air.
is the mass density of air.
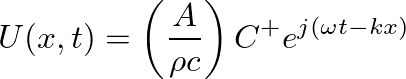 (20)
(20)
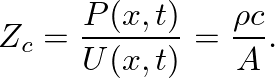 (21)
(21)

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |