Digital Filtering

Digital filters are fundamental to digital audio processing. While we only have time here for a short overview of the essential features of filters, students are encouraged to pursue more advanced courses and references in filter analysis and design.

• The processing of signals is called filtering. When applied to discrete-time signals, this processing is called digital filtering.

• Digital filters are defined by their impulse response, $h[n]$, or the filter output given a unit sample impulse input signal. A discrete-time unit impulse signal is defined by:
  $$\delta[n] \ensuremath{\stackrel{\Delta}{=}}\left\{ \begin{array}{ll} 1, & n = 0 \\ 0, & n \neq 0 \end{array} \right.$$

• The filtering operation in the time domain is referred to as convolution, defined as
  $$y[n] = x[n] \ast h[n] = \sum_{m=-\infty}^{\infty} h[m] x[n-m],$$
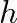  where $h$ is the filter impulse response and 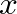$x$ is the input signal to the filter.

• Digital filters are often more intuitively understood in terms of their frequency response. That is, how is a sinusoidal signal of a given frequency affected by the filter.

• One way to find the frequency response of a digital filter is by taking the DFT (or FFT) of the filter impulse response.

• The frequency response of a filter consists of its magnitude and phase responses. The magnitude response indicates the ratio of a filtered sine wave's output amplitude to its input amplitude. The phase response describes the phase “offset” or time delay experienced by a sine wave passing through a filter.