Next: Sinusoidal Oscillators Up: MUMT 307: Week #4 Previous: MUMT 307: Week #4
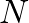 samples, a sample rate of
samples, a sample rate of 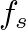 samples per second, and a phase increment
samples per second, and a phase increment 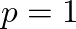 sample per time step, the output signal will have a fundamental frequency of
sample per time step, the output signal will have a fundamental frequency of 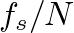 (assuming the wavetable holds only one period of the waveform).
(assuming the wavetable holds only one period of the waveform).
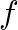 is given by
is given by 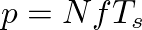 , where
, where 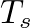 is the sample period.
is the sample period.
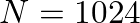 samples and your sample rate is
samples and your sample rate is 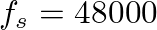 samples per second, the fundamental frequency
samples per second, the fundamental frequency 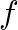 will be 46.875 Hz with
will be 46.875 Hz with 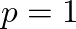 . If
. If 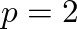 , you will read through the table twice as many times in the same time duration, so the resultant frequency will be 93.75 Hz. More generally, if you want
, you will read through the table twice as many times in the same time duration, so the resultant frequency will be 93.75 Hz. More generally, if you want 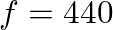 Hz, then the pointer needs to jump by 9.387 samples in the buffer per time step (
Hz, then the pointer needs to jump by 9.387 samples in the buffer per time step (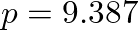 ) to produce the desired frequency.
) to produce the desired frequency.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |