Next: The Discrete Fourier Transform (DFT) Up: Discrete-Time Signals & Digital Filtering Previous: Discrete-Time Signals
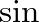 or
or 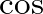 functions; in the frequency domain, they consist of a single non-zero frequency component.
functions; in the frequency domain, they consist of a single non-zero frequency component.
![$\displaystyle \delta[n] \ensuremath{\stackrel{\Delta}{=}}\left\{ \begin{array}{ll} 1, & n = 0 \\
0, & n \neq 0 \end{array} \right.
$](img21.png)
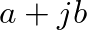 , which can be plotted in terms of magnitude and phase values. Magnitude values are calculated as
, which can be plotted in terms of magnitude and phase values. Magnitude values are calculated as
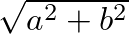 , while phase values are calculated as
, while phase values are calculated as
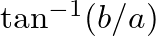 .
.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |