The Finite Difference technique replaces derivative expressions in differential equations with discrete-time difference approximations.
- The backward finite difference
(FD) approximation is given by:
where T is the sampling period.
- In the frequency-domain, the FD approximation is defined by the mapping:
where s is the Laplace Transform frequency variable and z is the z-Transform frequency variable.
- The inverse finite difference substitution is given by:
- The FD approximation maps analog dc (s=0) to digital dc (z=1).
- By noting that the FD approximation maps an infinite analog frequency (
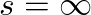 ) to z=0, it should be clear that non-zero poles and zeros are warped in potentially undesireable ways.
) to z=0, it should be clear that non-zero poles and zeros are warped in potentially undesireable ways.
- The FD approximation does not alias because the conformal mapping
s = 1 - z-1 is one to one.
- By applying the FD twice, the second derivative is found as:
- The Matlab example, msd_fd.m, demonstrates the use of the finite difference approach to simulate the motion of the mass-spring-damper system.

| ©2004-2024 McGill University. All Rights Reserved.
Maintained by Gary P. Scavone.
|
![$\displaystyle \frac{d}{dt}x(t) \stackrel{\Delta}{=} \lim_{\delta \rightarrow 0} \frac{x(t) - x(t-\delta)}{\delta} \approx \frac{x[n] - x[n-1]}{T_s}
$](img52.png)
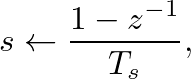
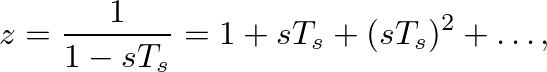
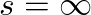 ) to z=0, it should be clear that non-zero poles and zeros are warped in potentially undesireable ways.
) to z=0, it should be clear that non-zero poles and zeros are warped in potentially undesireable ways.
![$\displaystyle \frac{d^2}{dt^2}x(t) \approx \frac{x[n] - 2 x[n-1] +x[n-2]}{T_s^2}
$](img56.png)
