Next: Finite-Differences vs. the Bilinear Transform Up: Discretization Methods: Previous: Centered Finite Differences
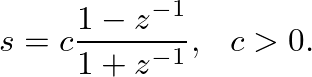
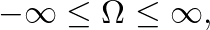 onto the discrete-time frequency space
onto the discrete-time frequency space
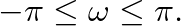 Continuous-time dc (
Continuous-time dc (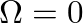 ) maps to discrete-time dc (
) maps to discrete-time dc (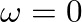 ) and infinite continuous-time frequency (
) and infinite continuous-time frequency (
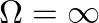 ) to the Nyquist frequency (
) to the Nyquist frequency (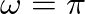 ). Thus, a nonlinear warping of the frequency axes occurs.
). Thus, a nonlinear warping of the frequency axes occurs.
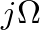 -axis in the s plane is mapped exactly once around the unit circle of the z plane, no aliasing occurs.
-axis in the s plane is mapped exactly once around the unit circle of the z plane, no aliasing occurs.
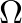 as
as
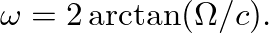
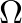 ) to the equivalent “digital” frequency (
) to the equivalent “digital” frequency (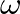 ), the constant c is found as
), the constant c is found as
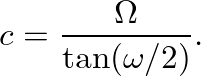

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |