Next: Complex Exponentials and “Orthogonality” Up: Spectral Analysis Previous: Sinusoidal “Dot-Products”
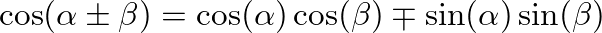 (4)
(4)
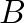 and
and  are constants proportional to the amplitude
are constants proportional to the amplitude 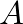 and the phase offset
and the phase offset 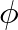 .
.
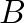 and
and  above and from which we can also calculate the amplitude
above and from which we can also calculate the amplitude 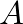 and the phase offset
and the phase offset 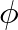 ).
).

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |