Next: The DFT Up: Spectral Analysis Previous: Fixing the Phase Problem
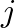 in front of the sine term. The Euler formula distinguishes the two terms using this notation, which effectively maps the result onto a two-dimensional complex space for each evaluated frequency.
in front of the sine term. The Euler formula distinguishes the two terms using this notation, which effectively maps the result onto a two-dimensional complex space for each evaluated frequency.
![$\displaystyle \langle x_n, y_n \rangle = \sum_{n=0}^{N-1} x[n] y^{\ast}[n],
$](img43.png) (8)
(8)
![$y^{\ast}[n]$](img44.png) denotes the complex conjugate of
denotes the complex conjugate of ![$y[n]$](img14.png) .
.
![$x[n]$](img1.png) with itself produces a real value:
with itself produces a real value:
![$\displaystyle \langle x_n, x_n \rangle = \sum_{n=0}^{N-1} x[n] x^{\ast}[n] = \sum_{n=0}^{N-1}\left\vert x[n] \right\vert^2.
$](img45.png) (9)
(9)
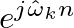 , we can easily show that
, we can easily show that
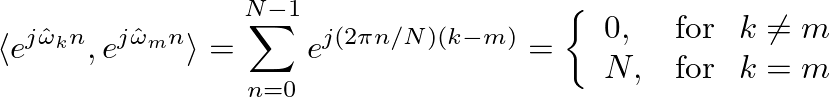 (10)
(10)
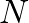 (instead of
(instead of 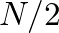 ).
).

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |