Next: The Short-Time Fourier Transform Up: Spectral Analysis Previous: The DFT
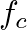 and
and 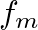 results in a signal with two spectral components at frequencies
results in a signal with two spectral components at frequencies 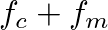 and
and 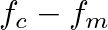 .
.
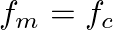 , the result will be two spectral components at frequencies of 0 and 2
, the result will be two spectral components at frequencies of 0 and 2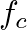 .
.
![$x[n]$](img1.png) by a rectangular “window” (a sequence of ones of length
by a rectangular “window” (a sequence of ones of length 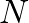 ).
).
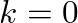 (or DC).
(or DC).
![$x[n]$](img1.png) at frequencies
at frequencies
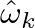 down to
down to 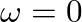 , where their relative strengths are then “extracted” by means of a very narrow lowpass filter.
, where their relative strengths are then “extracted” by means of a very narrow lowpass filter.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |