Next: The Heterodyning Interpretation Up: Spectral Analysis Previous: Complex Exponentials and “Orthogonality”
![$x[n]$](img1.png) and
and 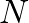 complex exponential signals representing sine and cosine terms at discrete frequencies
complex exponential signals representing sine and cosine terms at discrete frequencies 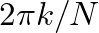 . Each of these inner product computations produces a single complex valued “weight” that indicates the relative strength of a specific sinusoidal frequency in the signal.
. Each of these inner product computations produces a single complex valued “weight” that indicates the relative strength of a specific sinusoidal frequency in the signal.
 DFT.
DFT.
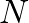 of the signal
of the signal ![$x[n]$](img1.png) . These frequencies are evenly distributed from 0 to
. These frequencies are evenly distributed from 0 to
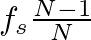 , so that the larger the value of
, so that the larger the value of 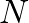 , the more precise the estimate of frequency content in the signal. However, from the sampling theorem, only those frequency components less than or equal to
, the more precise the estimate of frequency content in the signal. However, from the sampling theorem, only those frequency components less than or equal to 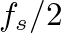 are unique.
are unique.
![$x[n]$](img1.png) would have to be periodic and only contain frequency components that are integral multiples of
would have to be periodic and only contain frequency components that are integral multiples of 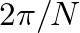 .
.
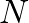 samples.
samples.
![$x[n]$](img1.png) is not periodic in
is not periodic in 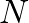 , the DFT will only provide an approximation of its actual frequency content.
, the DFT will only provide an approximation of its actual frequency content.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |