Next: Simple FM Example Algorithms Up: Frequency Modulation (FM) Synthesis Previous: The Mathematics of FM
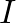 ) generally increases the effective bandwidth of the FM spectrum.
) generally increases the effective bandwidth of the FM spectrum.
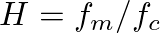 .
.
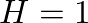 , the carrier and modulator frequencies are equal and the resulting spectrum is harmonic, with the fundamental frequency equal to the carrier frequency (
, the carrier and modulator frequencies are equal and the resulting spectrum is harmonic, with the fundamental frequency equal to the carrier frequency (
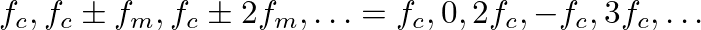 ).
).
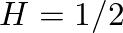 , the carrier frequency is double the modulator frequency and the resulting spectrum is harmonic, though with fundamental frequency equal to the modulator frequency.
, the carrier frequency is double the modulator frequency and the resulting spectrum is harmonic, though with fundamental frequency equal to the modulator frequency.
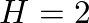 , the spectrum is harmonic with odd integer multiples of the fundamental
, the spectrum is harmonic with odd integer multiples of the fundamental  .
.
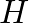 has the form
has the form 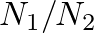 , where
, where 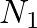 and
and 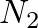 are positive integers, the resulting spectrum will be harmonic.
are positive integers, the resulting spectrum will be harmonic.
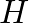 is not of this form, the spectrum will be inharmonic.
is not of this form, the spectrum will be inharmonic.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |