Next: Tapped Delay Lines Up: Delay Lines Previous: Delay Line Interpolation: Linear Interpolation
![\begin{eqnarray*}
\hat{x}[n-\Delta] \ensuremath{\stackrel{\Delta}{=}}y[n] &=& a ...
...[n-1] - a \cdot y[n-1] \\
&=& a \cdot (x[n] - y[n-1]) + x[n-1].
\end{eqnarray*}](img101.png)
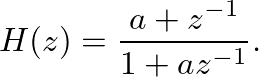
 , the delay becomes
, the delay becomes
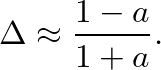
 , the allpass coefficient
, the allpass coefficient 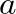 is determined as
is determined as
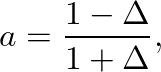
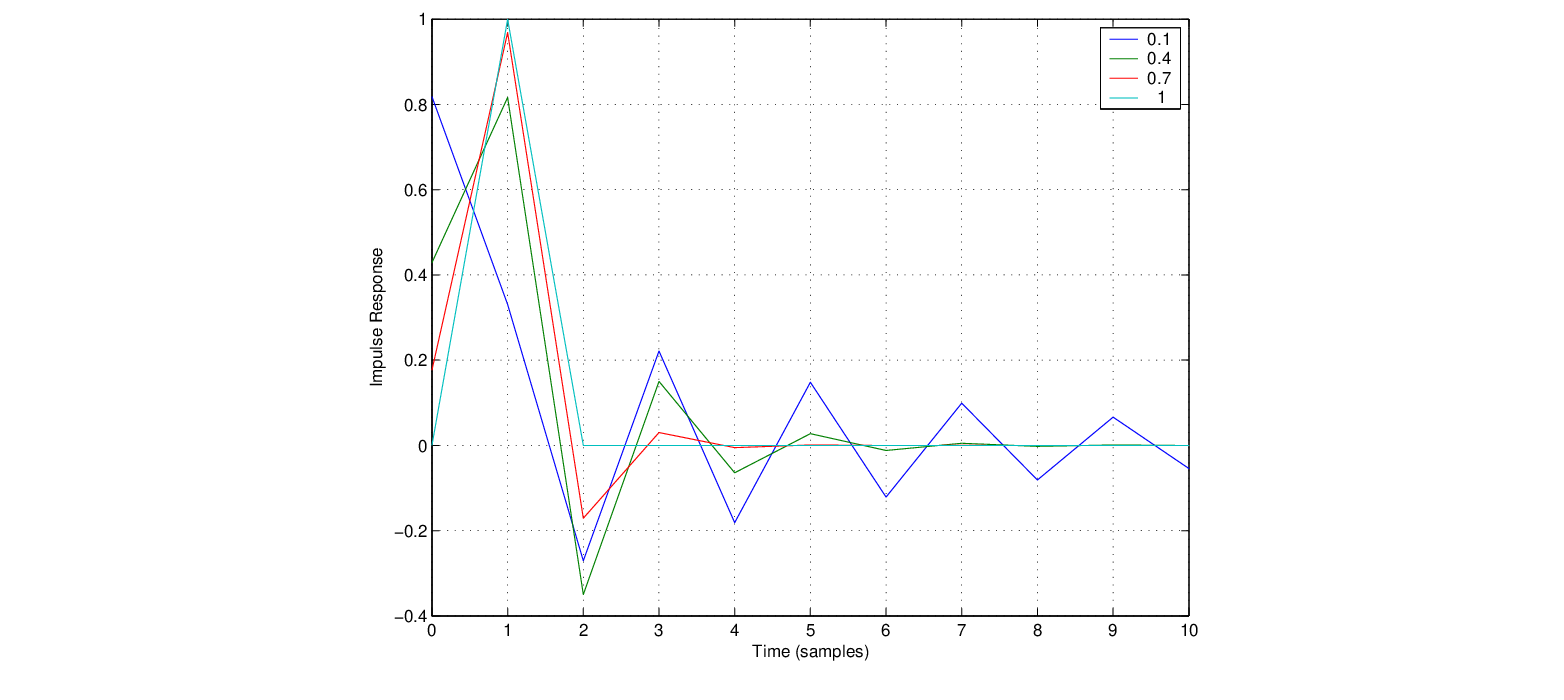
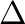 is best maintained in the range
is best maintained in the range
 to achieve maximally flat phase delay response together with the fastest decaying impulse response, a desired characteristic when dealing with dynamic delay values and their associated transient responses.
to achieve maximally flat phase delay response together with the fastest decaying impulse response, a desired characteristic when dealing with dynamic delay values and their associated transient responses.
 closer to 0.0 have significantly longer transient “tails”.
closer to 0.0 have significantly longer transient “tails”.
 |

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |