Next: Delay Line Interpolation: Allpass Interpolation Up: Delay Lines Previous: Feedback Comb Filters
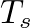 , it is possible to apply interpolation techniques to approximate values between those in memory.
, it is possible to apply interpolation techniques to approximate values between those in memory.
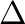 be a number between 0 and 1 that indicates how far to interpolate a signal
be a number between 0 and 1 that indicates how far to interpolate a signal 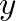 between time
between time 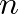 and time
and time 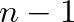 . The linearly interpolated value
. The linearly interpolated value
![$\hat{y}[n-\Delta]$](img97.png) is given by:
is given by:
![\begin{eqnarray*}
\hat{y}[n-\Delta] &=& (1 - \Delta) \cdot y[n] + \Delta \cdot y[n-1] \\
&=& y[n] + \Delta \cdot (y[n-1] - y[n]).
\end{eqnarray*}](img98.png)
 |

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |