Next: Digital Filtering Up: Discrete-Time Signals & Digital Filtering Previous: Frequency-Domain Representation and Ideal Signals
![$x[n]$](img15.png) , we can determine its frequency response using the Discrete Fourier Transform (DFT):
, we can determine its frequency response using the Discrete Fourier Transform (DFT):
![$\displaystyle X[k] \ensuremath{\stackrel{\Delta}{=}}\sum^{N-1}_{n=0}x[n] e^{-j 2 \pi k n / N}, \hspace{0.2in} k = 0, 1, 2, \ldots, N - 1.
$](img26.png)
![$\displaystyle x[n] = \frac{1}{N} \sum^{N-1}_{k=0}X[k] e^{j 2 \pi k n / N}, \hspace{0.2in} n = 0, 1, 2, \ldots, N - 1.
$](img27.png)
![$x[n]$](img15.png) onto a set of
onto a set of 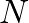 sampled complex sinusoids or sinusoidal basis functions at (normalized) radian frequencies given by
sampled complex sinusoids or sinusoidal basis functions at (normalized) radian frequencies given by
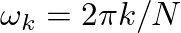 with
with
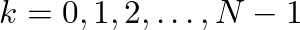 .
.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |