Digital filters
are fundamental to digital audio processing. While we only have time here for a cursory overview of the essential features of filters, students are encouraged to pursue more advanced courses and references in filter analysis and design.
- In general, we need to manipulate our signals. Even if we only seek to measure and analyze “real world” signals, we still typically need to “process” these signals in order to compensate for measurement system “biases”.
- The processing of signals is called filtering. When applied to discrete-time signals, this processing is called digital filtering.
- Digital filters are defined by their impulse response,
![$h[n]$](img31.png) , or the filter output given a unit sample impulse input signal.
, or the filter output given a unit sample impulse input signal.
- The filtering operation in the time domain is referred to as convolution, defined as
where
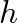 is the filter impulse response and
is the filter impulse response and 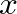 is the input signal to the filter.
is the input signal to the filter.
- Digital filters are often more intuitively understood in terms of their frequency response. That is, how is a sinusoidal signal of a given frequency affected by the filter.
- One way to find the frequency response of a digital filter is by taking the DFT of the filter impulse response, assuming the impulse response has sufficiently decayed before being truncated.
- The frequency response of a filter consists of its magnitude and phase responses. The magnitude response indicates the ratio of a filtered sine wave's output amplitude to its input amplitude. The phase response describes the phase “offset” or time delay in radians experienced by a sine wave passing through a filter.
- If the input to a filter is a sinusoid, the output from the filter will also be a sinusoid of the same frequency, though potentially scaled in amplitude or shifted in time. This is a fundamental property of linear systems.

| ©2004-2024 McGill University. All Rights Reserved.
Maintained by Gary P. Scavone.
|
![$h[n]$](img31.png) , or the filter output given a unit sample impulse input signal.
, or the filter output given a unit sample impulse input signal.
![$\displaystyle y[n] = x[n] \ast h[n] = \sum_{m=-\infty}^{\infty} h[m] x[n-m],
$](img32.png)
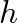 is the filter impulse response and
is the filter impulse response and 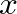 is the input signal to the filter.
is the input signal to the filter.
