Next: Infinite Impulse Response (IIR) Filters Up: Discrete-Time Signals & Digital Filtering Previous: Filter Types and Descriptions
![$\displaystyle y[n] = b_{0} x[n] + b_{1} x[n - 1] + b_{2} x[n - 2] \ldots, \hspace{0.2in} n = 0, 1, 2, \ldots,
$](img39.png)
![$x[n] \ensuremath{\stackrel{\Delta}{=}}0$](img17.png) and output
and output
![$y[n] \ensuremath{\stackrel{\Delta}{=}}0$](img40.png) for
for 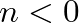 .
.
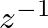 terms represent unit delays. Note that while this representation for a delay element is common and widely accepted in the signal processing community, the specification of delay in terms of powers of
terms represent unit delays. Note that while this representation for a delay element is common and widely accepted in the signal processing community, the specification of delay in terms of powers of 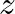 is a
is a 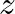 -domain characterization (to be described below) while the block diagram itself is a time-domain representation.
-domain characterization (to be described below) while the block diagram itself is a time-domain representation.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |