Next: Steady State and Transient Response Up: Discrete-Time Signals & Digital Filtering Previous: Finite Impulse Response (FIR) Filters
![$\displaystyle y[n] = b_{0} x[n] + b_{1} x[n - 1] + b_{2} x[n - 2] \ldots - a_{1} y[n - 1] - a_{2} y[n - 2] \ldots, \hspace{0.2in} n = 0, 1, 2, \ldots,
$](img43.png)
![$x[n] \ensuremath{\stackrel{\Delta}{=}}0$](img17.png) and output
and output
![$y[n] \ensuremath{\stackrel{\Delta}{=}}0$](img40.png) for
for 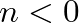 .
.
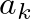 terms).
terms).

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |