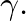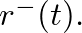A frequency-domain, transfer-matrix method for modeling piece-wise conical sections, as previously presented for cylindrical sections, is possible. The matrix elements are a bit more complicated, but the approach is well documented and validated and can include accurate characterizations of thermoviscous losses. In this section, however, we focus on the time-domain, traveling-wave approach for modeling combinations of conical sections.
Figure 10:
Junction of two conical tube sections.
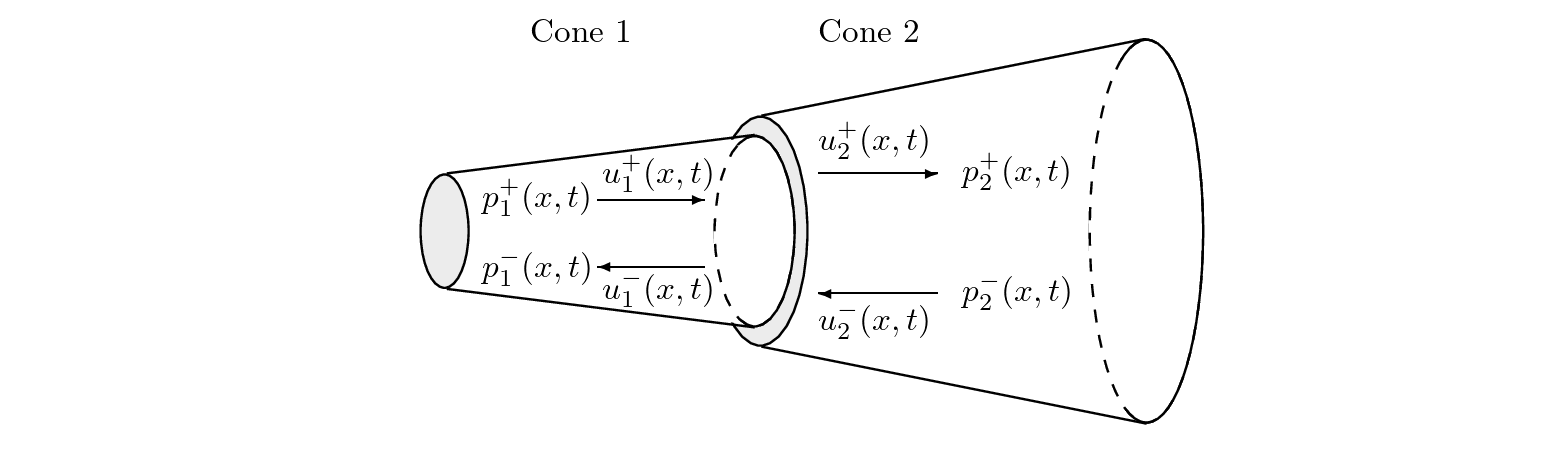 |
- At the boundary of two discontinuous and lossless conical sections, Fig. 10, the abrupt change in diameter and rate of taper will cause scattering of traveling wave components.
- Assuming continuity of pressure and conservation of volume flow at the boundary,
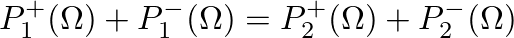 (29)
(29)
and
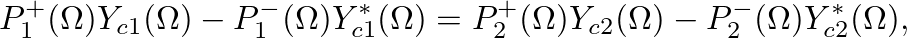 (30)
(30)
where 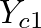 is the characteristic admittance for section
is the characteristic admittance for section  at the boundary looking in the positive
at the boundary looking in the positive 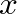 direction.
direction.
- The characteristic admittance for spherical waves in a cone is given by
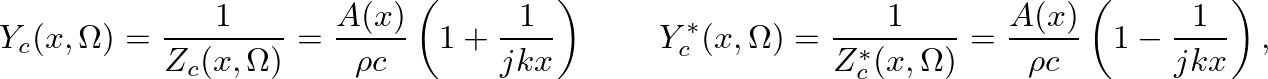 (31)
(31)
where
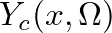 applies to traveling-wave components propagating away from the cone apex in the positive
applies to traveling-wave components propagating away from the cone apex in the positive 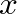 direction and
direction and
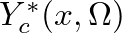 to traveling-wave components propagating toward the cone apex in the negative
to traveling-wave components propagating toward the cone apex in the negative 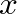 direction.
direction.
- Solving for
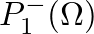 at the junction,
at the junction,
![$\displaystyle P_{1}^{-}(\Omega) = \left[\frac{Y_{c1}(\Omega) - Y_{c2}(\Omega)}{...
...st}(\Omega)}{Y_{c1}^{\ast}(\Omega) + Y_{c2}(\Omega)}\right] P_{2}^{-}(\Omega).
$](img159.png) (32)
(32)
- The frequency-dependent scattering coefficient that relates
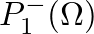 to
to
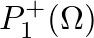 is
is
where 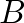 is the ratio of wave front surface areas
is the ratio of wave front surface areas 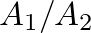 at the boundary and
at the boundary and 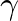 is given by
is given by
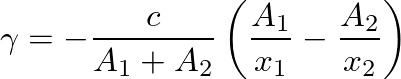 (34)
(34)
(Gilbert et al., 1990; Martínez and Agulló, 1988).
- This reflectance is given a negative superscript to indicate scattering in the negative
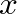 direction.
direction.
- The parameters
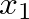 and
and 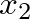 are measured from the (imaginary) apices of cones
are measured from the (imaginary) apices of cones 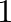 and
and 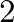 , respectively, to the discontinuity.
, respectively, to the discontinuity.
- Similarly, the expression for
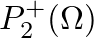 at the junction is
at the junction is
![$\displaystyle P_{2}^{+}(\Omega) = \left[\frac{Y_{c1}(\Omega) + Y_{c1}^{\ast}(\O...
...st}(\Omega)}{Y_{c2}(\Omega) + Y_{c1}^{\ast}(\Omega)}\right] P_{2}^{-}(\Omega),
$](img171.png) (35)
(35)
and the reflectance that relates
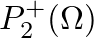 to
to
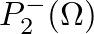 is
is
- This reflectance is given a positive superscript to indicate scattering in the positive
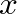 direction.
direction.
- The scattering equations can then be expressed in terms of
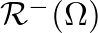 and
and
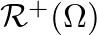 as
as
- It is possible to define transmittances that indicate scattering through the junction as
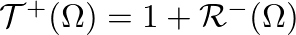 and
and
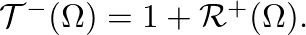
- These expressions are equally valid when either acoustic section is cylindrical, rather than conical. Replacing cone
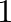 by a cylindrical section,
by a cylindrical section,
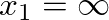 and
and 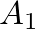 is given by the cylinder's cross-sectional area at the discontinuity.
is given by the cylinder's cross-sectional area at the discontinuity.
- Whereas the junction scattering coefficients for cylindrical bore diameter discontinuities were real and constant, these expressions are frequency-dependent and must be transformed to discrete-time filters for time-domain implementation.
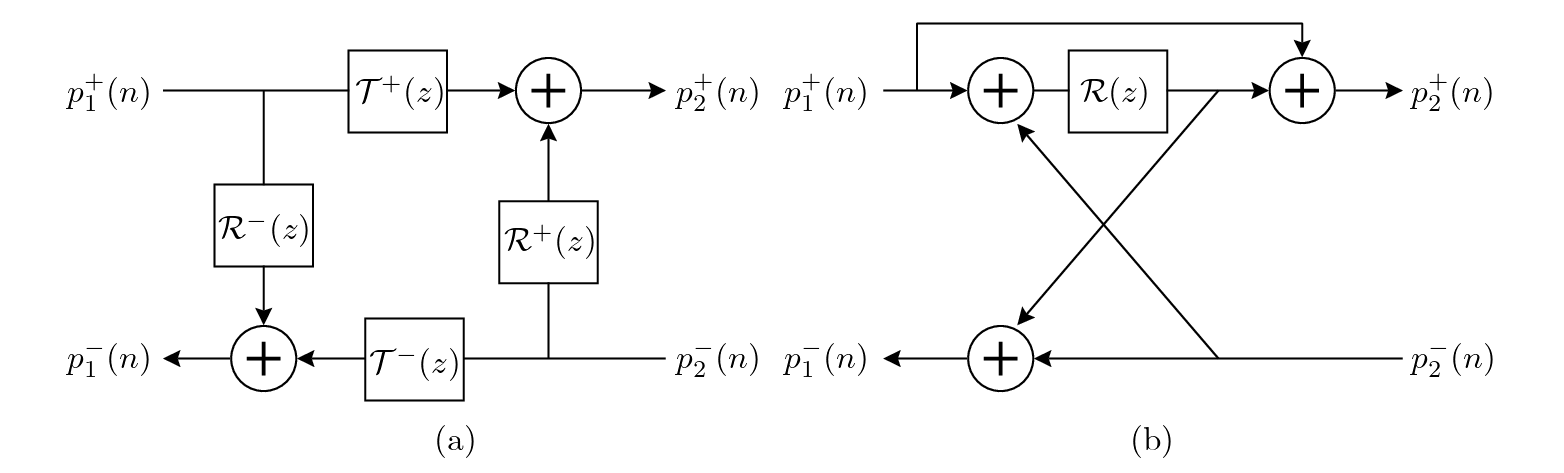
- Figure 11(a) illustrates the general scattering junction implementation for diameter and taper discontinuities in conical bores.
Figure 11:
(a) The scattering junction for diameter and taper discontinuities in conical bores; (b) The one-multiply scattering junction for a taper discontinuity only [after (Välimäki, 1995)].
 |
- Because
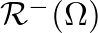 and
and
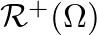 are different, the one-multiply form of the scattering junction implementation is not possible.
are different, the one-multiply form of the scattering junction implementation is not possible.
- However, if the wavefront surface areas are approximated by cross-sectional areas at the discontinuity, which is reasonable only for small changes in taper rate and cross-section, the reflectances
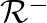 and
and
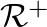 become identical for a discontinuity of taper only. In this case, a one-multiply scattering junction implementation is possible, as shown in Fig. 11(b) (Välimäki, 1995).
become identical for a discontinuity of taper only. In this case, a one-multiply scattering junction implementation is possible, as shown in Fig. 11(b) (Välimäki, 1995).
- Strictly speaking, however, the propagating wave fronts in cones are spherical and thus
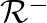 and
and
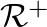 will never be identical, even for a simple taper discontinuity.
will never be identical, even for a simple taper discontinuity.
- Equation (33) can be transformed to the time domain, resulting in the reflection function
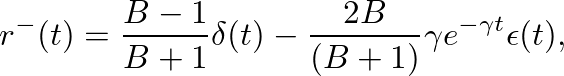 (39)
(39)
where 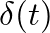 is the Dirac impulse and
is the Dirac impulse and 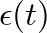 is the Heaviside unit step function (Martínez and Agulló, 1988).
is the Heaviside unit step function (Martínez and Agulló, 1988).
- An appropriate discrete-time filter is found by making the bilinear transform frequency variable substitution in Eq. (33) with the result
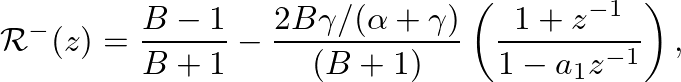 (40)
(40)
where 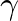 is as given in Eq. (34),
is as given in Eq. (34), 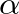 is the bilinear transform constant, and
is the bilinear transform constant, and
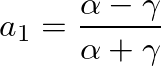 (41)
(41)
is the first-order filter pole location in the 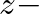 plane.
plane.
- Unfortunately,
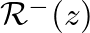 is unstable for negative
is unstable for negative 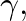 which occurs any time cone
which occurs any time cone 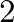 has a lower rate of taper than cone
has a lower rate of taper than cone 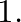
- Equivalently,
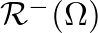 has no causal inverse Fourier transform for negative
has no causal inverse Fourier transform for negative 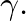
- This corresponds to a growing exponential in the reflection function
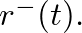
- The reflectance is a junction characteristic that is “blind” to the boundary conditions upstream or downstream from it. Physically realistic boundary conditions in such cases, however, will always limit the time duration over which the growing exponential can exist.
- Experimental measurements of reflection functions due to discontinuities have verified this general behavior (Agulló et al., 1995).
- The problem here in terms of digital waveguide modeling, is that the growing exponentials become unstable digital filters in the discrete-time domain.

| ©2004-2022 McGill University. All Rights Reserved.
Maintained by Gary P. Scavone.
|
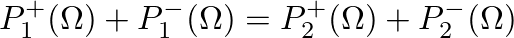 (29)
(29)
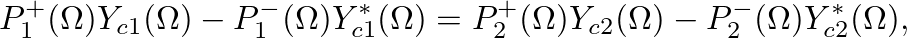 (30)
(30)
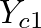 is the characteristic admittance for section
is the characteristic admittance for section 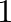 at the boundary looking in the positive
at the boundary looking in the positive 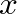 direction.
direction.
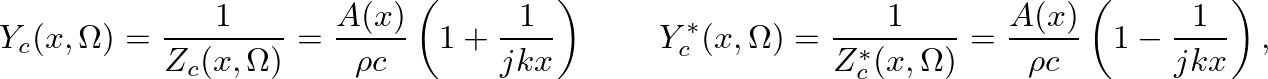 (31)
(31)
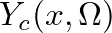 applies to traveling-wave components propagating away from the cone apex in the positive
applies to traveling-wave components propagating away from the cone apex in the positive 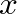 direction and
direction and
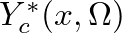 to traveling-wave components propagating toward the cone apex in the negative
to traveling-wave components propagating toward the cone apex in the negative 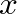 direction.
direction.
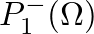 at the junction,
at the junction,
![$\displaystyle P_{1}^{-}(\Omega) = \left[\frac{Y_{c1}(\Omega) - Y_{c2}(\Omega)}{...
...st}(\Omega)}{Y_{c1}^{\ast}(\Omega) + Y_{c2}(\Omega)}\right] P_{2}^{-}(\Omega).
$](img159.png) (32)
(32)
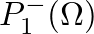 to
to
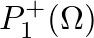 is
is
 is the ratio of wave front surface areas
is the ratio of wave front surface areas 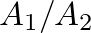 at the boundary and
at the boundary and 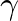 is given by
(Gilbert et al., 1990; Martínez and Agulló, 1988).
is given by
(Gilbert et al., 1990; Martínez and Agulló, 1988).
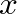 direction.
direction.
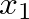 and
and 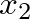 are measured from the (imaginary) apices of cones
are measured from the (imaginary) apices of cones 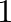 and
and 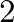 , respectively, to the discontinuity.
, respectively, to the discontinuity.
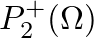 at the junction is
at the junction is
![$\displaystyle P_{2}^{+}(\Omega) = \left[\frac{Y_{c1}(\Omega) + Y_{c1}^{\ast}(\O...
...st}(\Omega)}{Y_{c2}(\Omega) + Y_{c1}^{\ast}(\Omega)}\right] P_{2}^{-}(\Omega),
$](img171.png) (35)
(35)
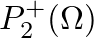 to
to
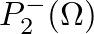 is
is
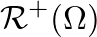

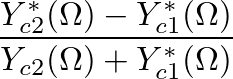

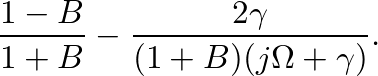
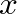 direction.
direction.
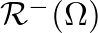 and
and
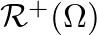 as
as
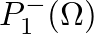

![$\displaystyle \mathcal{R}^{-}(\Omega) P_{1}^{+}(\Omega) + \left[1 + \mathcal{R}^{+}(\Omega) \right] P_{2}^{-}(\Omega)$](img179.png)
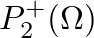

![$\displaystyle \left[1 + \mathcal{R}^{-}(\Omega) \right] P_{1}^{+}(\Omega) + \mathcal{R}^{+}(\Omega) P_{2}^{-}(\Omega).$](img181.png)
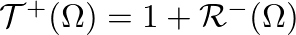 and
and
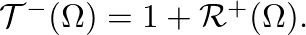
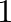 by a cylindrical section,
by a cylindrical section,
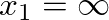 and
and 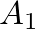 is given by the cylinder's cross-sectional area at the discontinuity.
is given by the cylinder's cross-sectional area at the discontinuity.

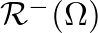 and
and
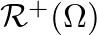 are different, the one-multiply form of the scattering junction implementation is not possible.
are different, the one-multiply form of the scattering junction implementation is not possible.
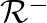 and
and
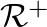 become identical for a discontinuity of taper only. In this case, a one-multiply scattering junction implementation is possible, as shown in Fig. 11(b) (Välimäki, 1995).
become identical for a discontinuity of taper only. In this case, a one-multiply scattering junction implementation is possible, as shown in Fig. 11(b) (Välimäki, 1995).
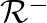 and
and
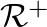 will never be identical, even for a simple taper discontinuity.
will never be identical, even for a simple taper discontinuity.
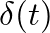 is the Dirac impulse and
is the Dirac impulse and 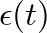 is the Heaviside unit step function (Martínez and Agulló, 1988).
is the Heaviside unit step function (Martínez and Agulló, 1988).
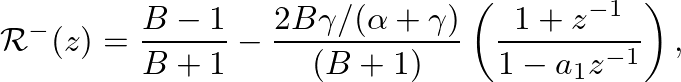 (40)
(40)
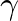 is as given in Eq. (34),
is as given in Eq. (34), 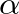 is the bilinear transform constant, and
is the bilinear transform constant, and
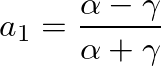 (41)
(41)
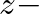 plane.
plane.
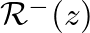 is unstable for negative
is unstable for negative 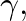 which occurs any time cone
which occurs any time cone 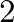 has a lower rate of taper than cone
has a lower rate of taper than cone 
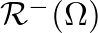 has no causal inverse Fourier transform for negative
has no causal inverse Fourier transform for negative