Next: Simulation Results Up: Bowed String Modeling Previous: The Bowing Mechanism
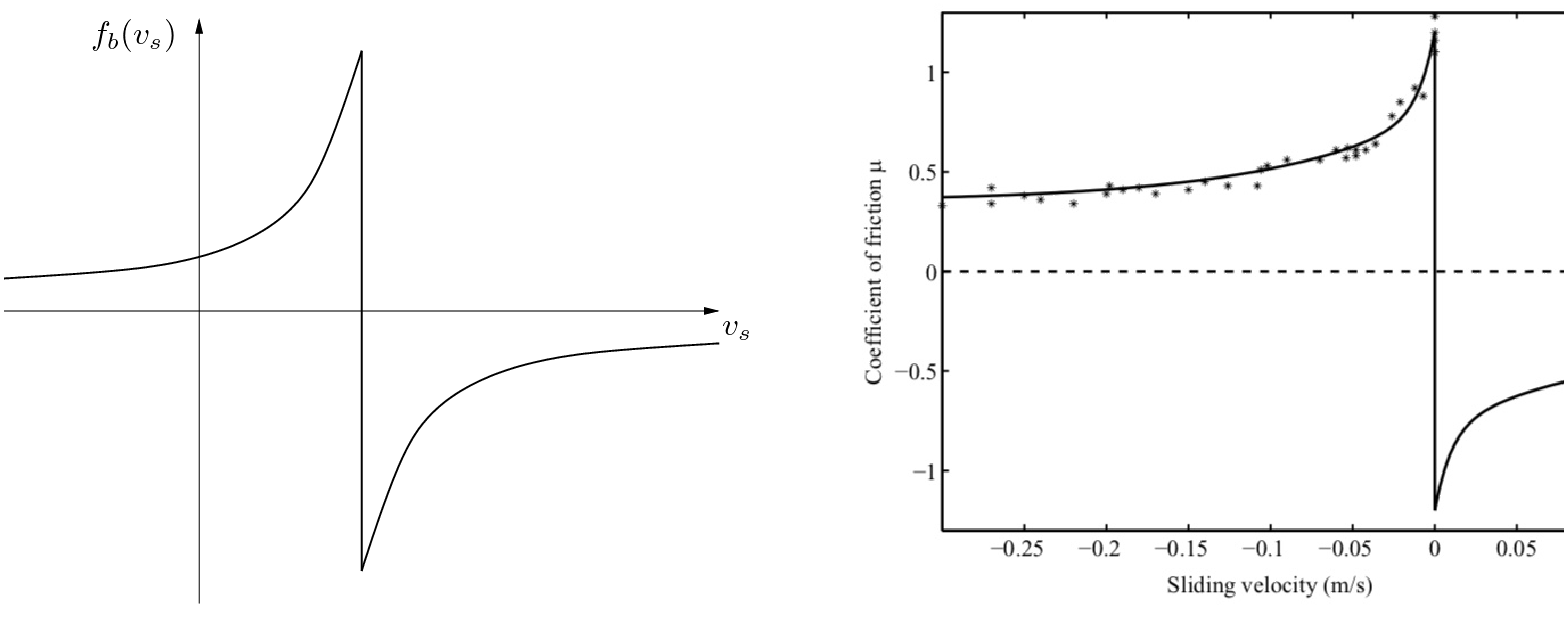 |
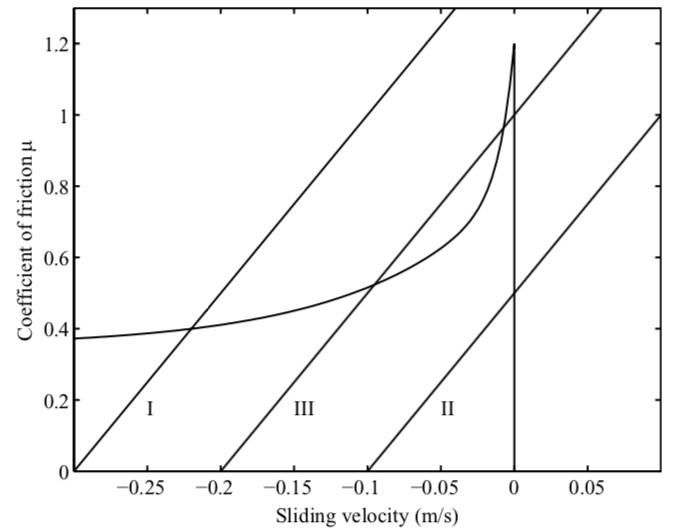
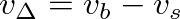 , the difference between the bow and string velocities.
, the difference between the bow and string velocities.
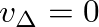 (the point of infinite slope in the figure). In this case, the friction force is based primarily on static friction.
(the point of infinite slope in the figure). In this case, the friction force is based primarily on static friction.
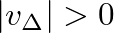 , the string is “slipping” and the friction force is based roughly on kinetic friction, which is significantly less than the static friction (especially when rosin is applied to the bow).
, the string is “slipping” and the friction force is based roughly on kinetic friction, which is significantly less than the static friction (especially when rosin is applied to the bow).
![$f_{s} = R_s [v_{s}^{+} - v_{s}^{-}] = R_s [v_{s} - 2v_{s}^{-}]$](img6.png) , where
, where 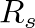 is the string wave impedance.
is the string wave impedance.
|

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |