Next: Perceptual Approach to Reverberation Simulation Up: Artificial Reverberation Previous: Artificial Reverberation
![\begin{figure}\begin{center}
\begin{picture}(3.9,3.7)
\put(0.3,0){\epsfig{file...
...){$h_{23}$}
\put(3.8,0.75){$y_{2}[n]$}
\end{picture} \end{center}
\end{figure}](img22.png) |
![$\displaystyle y_{i}[n] = \sum_{j=1}^{3} s_{j} \ast h_{ij}[n] = \sum_{j=1}^{3} \sum_{m=0}^{M_{ij}} s_{j}[m]h_{ij}[n-m], \hspace{0.2in} i = 1,2
$](img23.png)
where ![$h_{ij}[n]$](img24.png) is an FIR filter representation of the impulse response from source
is an FIR filter representation of the impulse response from source 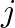 to ear
to ear 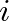 and
and 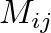 is the length of the filter.
is the length of the filter.
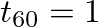 second) and a sample rate
second) and a sample rate 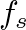 = 50 kHz, each filter would require 50,000 multiplies and additions per sample or 2.5 billion multiply-adds per second. For three sources and two listening points (ears), this corresponds to 30 billion operations per second.
= 50 kHz, each filter would require 50,000 multiplies and additions per sample or 2.5 billion multiply-adds per second. For three sources and two listening points (ears), this corresponds to 30 billion operations per second.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |