Next: Wave Equation Solutions Up: Wave Motion in Strings Previous: Wave Motion in Strings
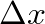 ) is
) is
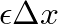 , where
, where 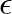 is the mass per unit length of the string.
is the mass per unit length of the string.
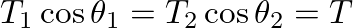 .
.
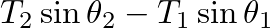 .
.
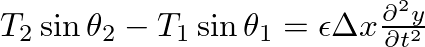 .
.
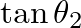 and
and
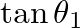 are the slopes of the string at the points
are the slopes of the string at the points 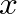 and
and 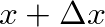 :
:
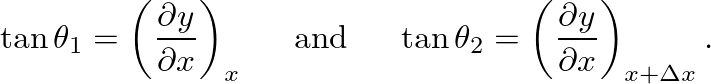
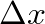 ,
,
![$\displaystyle \frac{1}{\Delta x} \left[\left( \frac{\partial y}{\partial x}\rig...
...x}\right)_x \right] = \frac{\epsilon}{T} \frac{\partial^{2}y}{\partial t^{2}}.
$](img16.png)
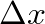 approach zero, we obtain the linear partial differential equation
approach zero, we obtain the linear partial differential equation
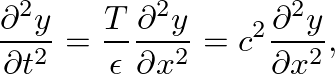
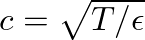 is the speed of wave motion on the string. This is the one-dimensional wave equation that describes small amplitude, lossless transverse waves on a stretched string.
is the speed of wave motion on the string. This is the one-dimensional wave equation that describes small amplitude, lossless transverse waves on a stretched string.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |