Next: Standing Waves Up: Wave Motion in Strings Previous: The 1D Wave Equation
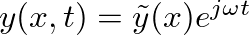 , where
, where 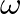 is radian frequency and
is radian frequency and 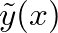 represents the spatial distribution of the complex amplitude displacement.
represents the spatial distribution of the complex amplitude displacement.
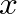 alone).
alone).
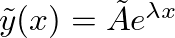 , which after substitution yields:
, which after substitution yields:
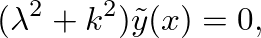
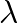 is the wavelength and
is the wavelength and
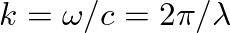 is the wavenumber, which represents spatial frequency in radians per meter.
is the wavenumber, which represents spatial frequency in radians per meter.
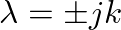 , leading to a complete solution of the form:
, leading to a complete solution of the form:
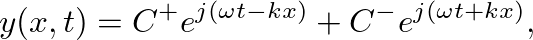
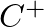 and
and 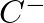 are complex amplitudes.
are complex amplitudes.
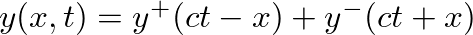 .
.
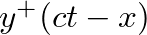 represents a wave traveling in the positive
represents a wave traveling in the positive 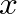 direction with a velocity
direction with a velocity 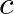 . Similarly,
. Similarly, 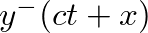 represents a wave traveling in the negative
represents a wave traveling in the negative 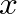 direction with the same velocity. Each component is generally referred to as a traveling wave.
direction with the same velocity. Each component is generally referred to as a traveling wave.
 and
and 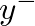 are arbitrary and of fixed shape (given our assumed lossless medium) ... see waves on string simulation.
are arbitrary and of fixed shape (given our assumed lossless medium) ... see waves on string simulation.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |