Next: Impedance Up: Wave Motion in Strings Previous: Wave Equation Solutions
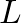 that is rigidly fixed at
that is rigidly fixed at 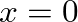 and
and 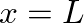 . This implies boundary conditions of
. This implies boundary conditions of 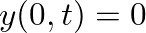 and
and 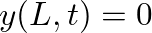 .
.
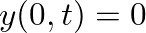 and Eq. (3), we find that
and Eq. (3), we find that 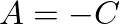 and
and 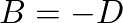 , so
, so
![$\displaystyle y(x,t) = A [\sin (\omega t - kx) - \sin(\omega t + kx)] + B [\cos(\omega t - kx) - \cos (\omega t + kx)].
$](img48.png) (4)
(4)
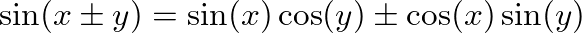 and
and
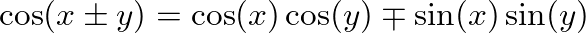 , we obtain
, we obtain
![\begin{eqnarray*}
y(x,t) &=& 2 A \sin(k x)\cos(\omega t) - 2 B \sin(k x)\sin((\omega t) \\
&=& 2 [A \cos(\omega t) - B \sin(\omega t)] \sin(k x).
\end{eqnarray*}](img51.png)
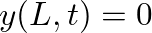 requires that
requires that 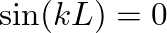 or
or
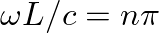 , so that
, so that 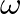 is restricted to values
is restricted to values
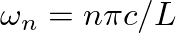 or
or
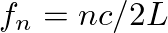 .
.
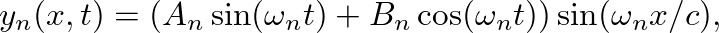 (5)
(5)
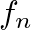 is a integer multiple
is a integer multiple 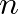 times
times 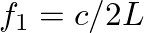 . These correspond to the well known standing wave patterns on a stretched string.
. These correspond to the well known standing wave patterns on a stretched string.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |