Next: The Driving Point Impedance of Up: Impedance Previous: Impedance
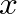 direction along an infinite string:
direction along an infinite string:
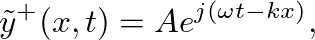
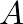 is a complex constant that describe the amplitude and phase of the traveling-wave component and
is a complex constant that describe the amplitude and phase of the traveling-wave component and
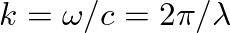 .
.
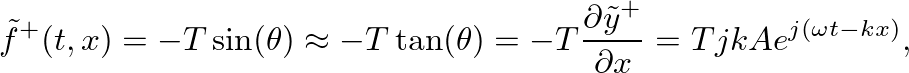
 is the string tension and
is the string tension and
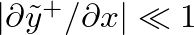 . This force is clearly balanced by an equal but opposite force exerted from the right-side portion of the string.
. This force is clearly balanced by an equal but opposite force exerted from the right-side portion of the string.
 is
is
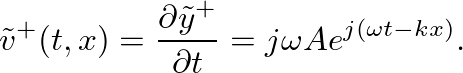
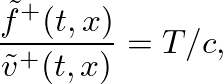
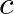 is the speed of wave propagation. In deriving the wave equation for string motion, we determined
is the speed of wave propagation. In deriving the wave equation for string motion, we determined
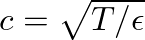 and thus
and thus 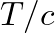 is also equal to
is also equal to 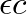 , where
, where 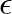 is the linear mass density of the string.
is the linear mass density of the string.
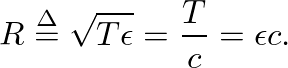
![$\displaystyle f(t,x) = R \left[ \frac{\partial}{\partial{t}} y^{+}(t - x/c) - \...
...l{t}} y^{-}(t + x/c)\right] = R \left[ v^{+}(t - x/c) - v^{-}(t + x/c)\right].
$](img72.png)
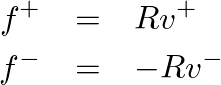

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |