Next: Digital Waveguide Theory Up: Impedance Previous: Wave Impedance
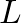 and tension
and tension 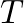 rigidly fixed at position
rigidly fixed at position 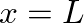 .
.
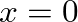 by a transverse sinusoidal force in the form of a complex exponential:
by a transverse sinusoidal force in the form of a complex exponential:
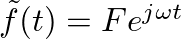 .
.
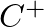 and
and 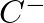 are complex constants that describe the amplitude and phase of each traveling-wave component with respect to the driving force and
are complex constants that describe the amplitude and phase of each traveling-wave component with respect to the driving force and
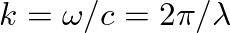 .
.
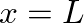 ), the boundary condition
), the boundary condition 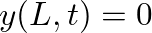 implies
implies
![$\displaystyle 0 = [C^{+} e^{-j k L} + C^{-} e^{j k L}] e^{j \omega t}.
$](img76.png)
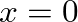 , the driving force must be compensated by a string force of
, the driving force must be compensated by a string force of
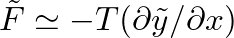 , resulting in the expression
, resulting in the expression
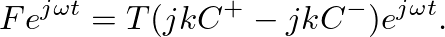
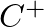 and
and 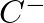 , which when substituted back into Eq. 6 gives
, which when substituted back into Eq. 6 gives
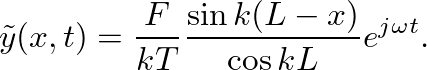
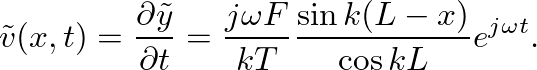
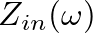 is defined as the ratio of force to velocity at the driving point (
is defined as the ratio of force to velocity at the driving point (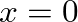 ):
):
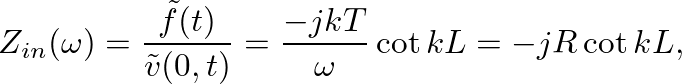
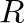 is the characteristic impedance of the string. This function is plotted below.
is the characteristic impedance of the string. This function is plotted below.
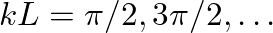 , and
, and 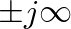 when
when
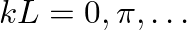 Note that this analysis does not account for any losses in the string or end support.
Note that this analysis does not account for any losses in the string or end support.
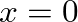 ) is fixed, the velocity of the string at that point must equal zero. This would correspond to an infinite impedance. Thus, the resonance frequencies of a string rigidly fixed at both its ends correspond to the frequencies at which
) is fixed, the velocity of the string at that point must equal zero. This would correspond to an infinite impedance. Thus, the resonance frequencies of a string rigidly fixed at both its ends correspond to the frequencies at which
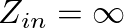 , or when
, or when
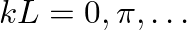 , from which we find the resonance frequencies
, from which we find the resonance frequencies
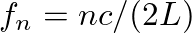 for
for
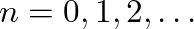 (which are the same as those found for the standing waves).
(which are the same as those found for the standing waves).
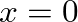 ) is perfectly free, the force of the string at that point must equal zero. This would correspond to an impedance of zero. Thus, the resonance frequencies of a string free on one end and rigidly fixed at the other correspond to the frequencies at which
) is perfectly free, the force of the string at that point must equal zero. This would correspond to an impedance of zero. Thus, the resonance frequencies of a string free on one end and rigidly fixed at the other correspond to the frequencies at which 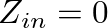 , or when
, or when
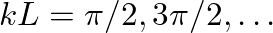 , from which we find the resonance frequencies
, from which we find the resonance frequencies
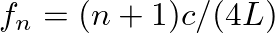 for
for
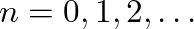 (which occur at odd integer multiples of the fundamental
(which occur at odd integer multiples of the fundamental
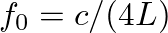 ).
).

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |