Next: Lumped Acoustic Elements Up: Acoustic Systems Previous: Hooke's Law for Plane Waves
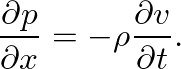
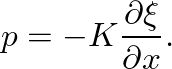
 and differentiate the second twice with respect to time
and differentiate the second twice with respect to time  , noting that particle velocity
, noting that particle velocity
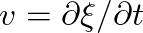 , we find
, we find
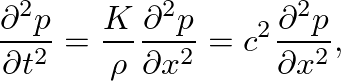 (6)
(6)

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |