Next: Cylindrical Air Column Acoustics Up: Acoustic Systems Previous: The Wave Equation for Plane
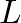 and
and 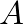 , respectively, then the enclosed air has a mass of
, respectively, then the enclosed air has a mass of 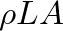 , where
, where 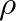 is the mass density of air.
is the mass density of air.
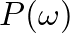 . Using Newton's second law (force = mass
. Using Newton's second law (force = mass  acceleration),
where
acceleration),
where
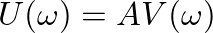 is the acoustic volume velocity of the air mass.
is the acoustic volume velocity of the air mass.
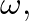 so that Eq. (7) reduces to
so that Eq. (7) reduces to
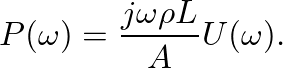 (8)
(8)
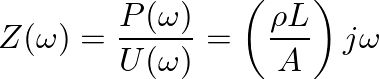 (9)
(9)
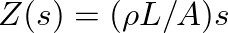 when expressed in terms of the Laplace transform), where initial conditions are assumed equal to zero.
when expressed in terms of the Laplace transform), where initial conditions are assumed equal to zero.
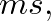 and thus the open tube has an equivalent acoustic “mass” equal to
and thus the open tube has an equivalent acoustic “mass” equal to 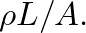 An inertance is also sometimes referred to as a constriction (Morse, 1981, p. 234).
An inertance is also sometimes referred to as a constriction (Morse, 1981, p. 234).
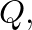 an increase in applied pressure
an increase in applied pressure 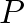 will decrease this volume by an amount
will decrease this volume by an amount 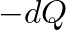 .
.
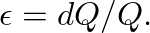 Using Hooke's law, we find
where
Using Hooke's law, we find
where 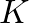 is the bulk modulus as discussed earlier.
is the bulk modulus as discussed earlier.
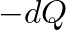 , in terms of the sinusoidal volume velocity
, in terms of the sinusoidal volume velocity 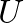 as
as
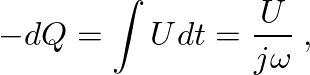 (11)
(11)
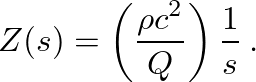 (12)
(12)
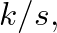 so by analogy the acoustic cavity has an equivalent “spring constant” equal to
so by analogy the acoustic cavity has an equivalent “spring constant” equal to 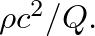
 , where
, where 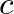 is the speed of sound in air,
is the speed of sound in air, 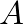 is the cross-sectional area of the tube,
is the cross-sectional area of the tube, 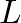 is the length of the tube, and
is the length of the tube, and 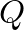 is the volume of the cavity.
is the volume of the cavity.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |